AI는 눈곱만큼도모름

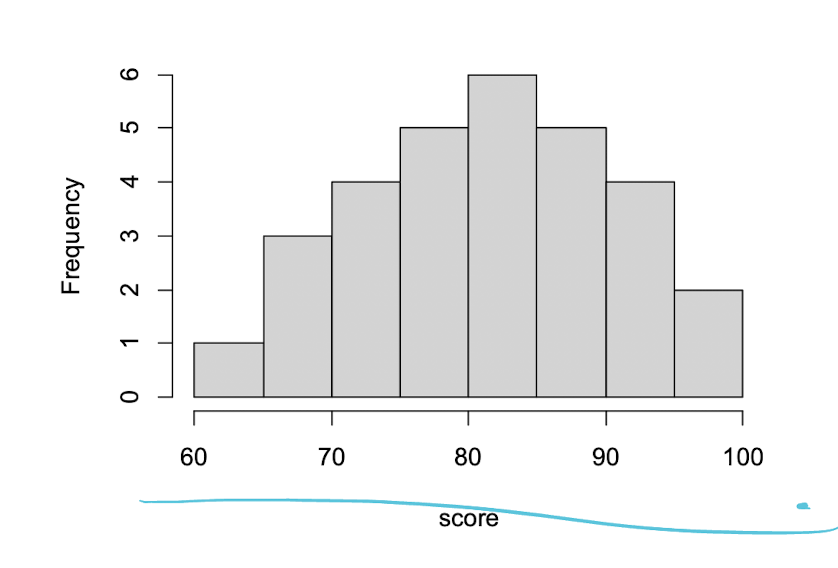
막대그래프그리기막대그래프 순서정렬 : fct_infreq()막대그래프 수치데이터 사용 :stat='identity'원그래프 In [ ]:install.packages('ggplot2')  Installing package into ‘/usr/local/lib/R/site-library’(as ‘lib’ is unspecified) In [ ]:install.packages('forcats')  Installing package into ‘/usr/local/lib/R/site-library’(as ‘lib’ is unspecified) In [ ]:library(ggplot2)library(forcats) # 막대 그래프 정렬  막대그래프 그리기¶질적변수 - 명목형변수 In [ ]:transp  In [..

1. 변수2. 질적 데이터의 요약-막대그래프 3. 양적 데이터의 요약 - 히스토그램 4. 양적 데이터의 요약-점도표, 평균, 분산1. 변수변수의 종류질적 변수(qualitative variable, 범주형 변수): 유한개 의 범주 중 하나의 값을 취하는 변수 ex) 성별, 학력양적 변수(quantitative variable): 양적인 수치로 측 정되는 변수 ex) 나이, 몸무게질적 변수의 종류명목형 변수(nominal variable): 범주들에 의미 있는 순서 를 정할 수 없는 질적 변수 ex) 성별순서형 변수(ordinal variable): 범주 간의 의미 있는 순서 를 정할 수 있는 질적 변수 ex) 학력양적 변수의 종류연속형 변수(continuous variable): 어떤 실수 구간 안의 모..

모집단(population): 관심 대상이 되는 모든 개체의 모임 표본(sample): 모집단을 알기 위해 실제로 관측한 모집단의 일부모수(parameter): 모집단의 특성을 나타내는 대푯값 통계량(Statistic): 표본의 특성을 나타내는 대푯값 표봉과 통계량모집단을 잘 반영하는 표본을 뽑는 것은 매우 중요하다 단순랜덤표집(simple random sampling): 유한모집단에서 m 개의 개체로 이루어진 가능한 모든 부분집합이 표본으로 선택될 확률이 같도록 설계된 표본 표집 방법통계량:모수를 추정하기 위해. 표본에서 얻은 값표본을 새로 뽑으면 통계량의 값이 달라진다

디렉토리 셋팅¶현재 위치 확인¶In [ ]:getwd()'/content'작업 디렉토리 셋팅하기¶In [ ]:setwd("/content") # / 혹은 \\ 로 경로 구분 사용.setwd("\\content") # Rstudio를 종료하면 헤제되기 때문에 다시 실행시 재설정 해주어야한다.R의 데이터 형태와 연산¶객체의 생성과 저장¶In [ ]:a 1 # b 1 # 단축키 : (masos) 'opt' + '-'c a + bVector (벡터)¶In [ ]:a c(1,2,3,4,5)b 1:5c seq(1,10,2) # 1에서 10까지 2 단위로d rep(10,5) # 10을 5번 반속e c(d,c)f c(1:4, seq(5,20,3))cat(' a : ',a,'\n','b..

주관적 확률 : 몇 번의 시행(경험)을 바탕으로 구함 (믿음의 정도)객관적 확률: 충분히 많은 시행을 바탕으로 구함 (빈도론적 확률, 통계적 확률)-> 시행 횟수가 많아지면 두 확률은 같아짐주관적 확률은 머피의 법칙과 같이 내가 우산을 가지고 나가는 날은 늘 비가안와나는 늘 주사위가 1이 나와 처럼충분히 많은 시행이 아닌 적은 시행에서 느끼는 확률적 경험을.이처럼 머피의 법칙의 발생 원인은 주관적 확률과 객관적 확률의 차이에서 기인한다. 객관적확률- 빈도론적 확률- 고전적 확률- 공리적 확률

set.seed(123) # 임의의 시드 값blood_types frequencysample_data A AB B O 13 17 13 7 # 상대도수 계산relative_frequency barplot(table(sample_data))pie(table(sample_data))

(문제1)어떤 사람이 동전 던지기를 200회 했는데 앞면이 90회 나왔다. 이때 상대도수적 관점의 확률은?(문제2)한 변 길이가 20cm인 정사각형 연못에 동전을 눈 감고 던질때 연못안의 한 변 길이가 10cm인 평평한 정사각형 조형물에 동전이 떨어진 확률은?(문제3)일정기간동안 1500명의 고객을 관찰한 결과 그중 700명이 그 회사제품을 구입했다.이때 고객이 제품 한 개를 구입할 확률은?(문제4)표본공간 S의 사건 A에 대한 확률을 P(A)라고 할 때 다음 주  공리적 확률 정의를 위한 조건이 아닌것은?1 . P(A) = \( \frac{사건 A에 속하는 원소의 개수}{표본공간의 전체 원소의 개수}\)2. 0 \leq P(A) \leq 13. P(S) = 14. \( A_{1}, A_{2},.....

- 확률(probability) : 어떤 사건이 일어날 가능성을 0과 1 사이의 실수로 표시한 것- 상대도수적 확률 : P(A)=\( \frac{사건 A가 발생한 횟수}{전체 시행 횟수} \)- 기하학적 확률    : P(A)=\( \frac{A 면적,길이}{전체 면적,길이} \)- 주관적 확률 : 어떤 사람이 경험 속에서 체감하는 확률수직선 또는 좌표평면에서의 확률을 기하학적 확률이라고 한다.위와 같은 표적지가 있을때 10점이 맞을 확률은\[ P(A)= \frac{원 A의 면적}{원 S의 면적}\]S의 반지름 : 50cm , A의 반지름 : 5cm\[ P(A) = \frac{\pi5^{2}}{\pi50^{2}} = \frac{1}{100}\]만약 표본공간S가 수직선이라면\[ P(A)..

- 확률(probability) : 어떤 사건이 일어날 가능성을 0과 1 사이의 실수로 표시한 것- 상대도수적 확률 : P(A)=\( \frac{사건 A가 발생한 횟수}{전체 시행 횟수} \)- 기하학적 확률    : P(A)=\( \frac{A 면적,길이}{전체 면적,길이} \)- 주관적 확률 : 어떤 사람이 경험 속에서 체감하는 확률통계학자 피어슨(Karl Pearson)은 동전던지기를 2만 4천번 해서 앞면이 나올 확률을 0.5005 =\( \left( \frac{12,012}{24,000} \right)\) 를 구하였다. 확률은 우연이 아닌 많은 수행을 통해 파악할 수 있는 일종의 질서라 할 수 있다. 이와 같은 확률을 정의하는 것을 상대도수적 정의라고 한다.(이론적 상대도수 확률의 계산)n번의 ..

R을 확률을 계산해서 주사위의 확률을 시각화 하기par(mfrow=c(2,2))# 2x2로 그림을 나눔# par = parameters# mfrow = multi-frame rowdice12 만약 주사위 중에 한번도 안나온 요소를 그래프에 표기 하고 싶다면 아래와 같이 factor을 이용한다.set.seed(42)dice12 par(mfrow=c(2,2))par 함수는 R에서 그래픽 장치의 매개변수를 설정하는 데 사용됩니다. 여러 가지 명령어를 사용하여 그래픽 장치의 여러 속성을 조정할 수 있습니다. 몇 가지 주요한 par 명령어는 다음과 같습니다:mfrow: 그래프를 여러 패널로 배열합니다. 예를 들어, par(mfrow=c(2, 2))는 2x2 패널 그리드로 설정합니다.mfcol: mfrow와 유사하..