- 확률(probability) : 어떤 사건이 일어날 가능성을 0과 1 사이의 실수로 표시한 것 - 상대도수적 확률 : P(A)=\( \frac{사건 A가 발생한 횟수}{전체 시행 횟수} \) - 기하학적 확률 : P(A)=\( \frac{A 면적,길이}{전체 면적,길이} \) - 주관적 확률 : 어떤 사람이 경험 속에서 체감하는 확률 |
수직선 또는 좌표평면에서의 확률을 기하학적 확률이라고 한다.
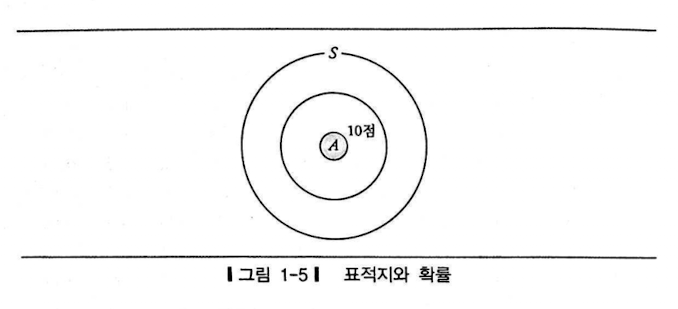
위와 같은 표적지가 있을때 10점이 맞을 확률은
\[ P(A)= \frac{원 A의 면적}{원 S의 면적}\]
S의 반지름 : 50cm , A의 반지름 : 5cm
\[ P(A) = \frac{\pi5^{2}}{\pi50^{2}} = \frac{1}{100}\]
만약 표본공간S가 수직선이라면
\[ P(A)= \frac{A의 길이}{S의 길이}\]
(문제1)
지하철역에서 120초 간격으로 지하철이 정차한다고 하자. 어떤 사람이 지하철역에 도착한 후 30초 이내 지하철을 탈 확률은?
(지하철 정차 시간은 무시한다)
(답1)
지하철 역에서 기다리는 시간에 대한 표본 공간
\[ S=\left\{t : 0\leq t \leq120\right\}\]
30초까지 기다리릴 사건
\[ A=\left\{t : 0\leq t \leq30\right\}\]
따라서 30초 이내 지하철을 찰 확률
\[ P(A) = \frac{30}{120}=\frac{1}{4}\]
(문제2)
8개의 같은 크기로 나눈 원판을 돌려서 한 지점을 선택하려고 한다. 이때 A지점이 선택될 확률을 구하여라.

(풀이)
\[ P(A) = \frac{A조각의 면적}{원 S의 면적}= \frac{\frac{1}{8\pi r^{2}}}{\pi r^{2}} =\frac{1}{8}\]
- Probability: The likelihood of an event occurring, expressed as a real number between 0 and 1. - Relative probability: P(A)=\( \frac{number of times event A occurs}{total number of trials} \) - Geometric probability: P(A)=\( \frac{A area,length}{total area,length} \) - Subjective probability: the probability that a person perceives in an experience. |
Probability on a vertical line or coordinate plane is called geometric probability.

Source: Concepts and Applications of Probability
The probability of hitting a 10 given a target like the one above is
\[ P(A)= \frac{area of circle A}{area of circle S}\]
Radius of S : 50cm , Radius of A : 5cm
\[ P(A) = \frac{\pi5^{2}}{\pi50^{2}} = \frac{1}{100}\]
If the sample space S is a vertical line
\[ P(A)= \frac{A's length}{S's length}\]
(Problem 1)
Suppose a subway stops every 120 seconds at a subway station. What is the probability that a person will take the subway within 30 seconds of arriving at the subway station?
(Ignore the duration of the subway stops)
(Answer 1)
Sample space for waiting time at a subway station
\[ S=\left\{t : 0\leq t \leq120\right\}\]
Events to wait up to 30 seconds
\[ A=\left\{t : 0\leq t \leq30\right\}\]
Probability of hitting the subway within 30 seconds
\[ P(A) = \frac{30}{120}=\frac{1}{4}\]
(Problem 2)
You want to spin a disk divided into eight equal parts and select a point. Find the probability that point A is selected.

(Solution)
\[ P(A) = \frac{Area of piece A}{Area of circle S}= \frac{\frac{1}{8\pi r^{2}}}{\pi r^{2}} =\frac{1}{8}\]
'Statistics > [강의정리] 확률의이해' 카테고리의 다른 글
| [확률의이해] 1장 R로하는 도수,상대도수, 도수분포표 (0) | 2024.04.21 |
|---|---|
| [확률의이해] 1장 확률의 기본 개념연습문제 (0) | 2024.04.21 |
| [확률의이해] 1장 확률의 기본 개념 - 1.3 확률의 상대도수적 정의 (0) | 2024.04.21 |
| [확률의이해] R을 이용한 주사위 확률과 그래프 (0) | 2024.04.21 |
| [확률의이해] 1장 확률의 기본 개념 - 1.2 확률의 개념 (0) | 2024.04.21 |