1. Introdution
2. Best Fitting Line
3. Simple Linear Regression
1. Introdution
1. Simple Linear Regression
■ 두 개의 연속적인(정량적인) 변수 간의 관계를 요약하고 연구할 수 있는 통계적 방법입니다.
- X로 표시되는 변수를 독립 변수로 이야기 하고 영어로는 predictor, explanatory variable, or independent variable 라고 불리며
- 다른 변수인 Y는 종속 변수로 response outcome or dependent variable라고 불립니다
(변수가 여러개일경우 -> 다중 선형 회귀분석(Multiple Linear Regression),
이상적인 변수일경우 -> Generalized Linear Model (GLM))
2. Deterministic Relationship(결정론적 관계)
■ 방정식은 두 변수 간의 관계를 정확하게 설명합니다.
- 원둘레 =\( \pi \) x 지름
- 옴의 법칙 I = \( \frac{V}{r} \)
-> 회귀분석에서는 이런 결정론적 관계가 아닌 통계적인 관계를 활용
3. Statistical Relationship (통계적 관계)
■ 변수 간의 관계는 완벽하지 않습니다.
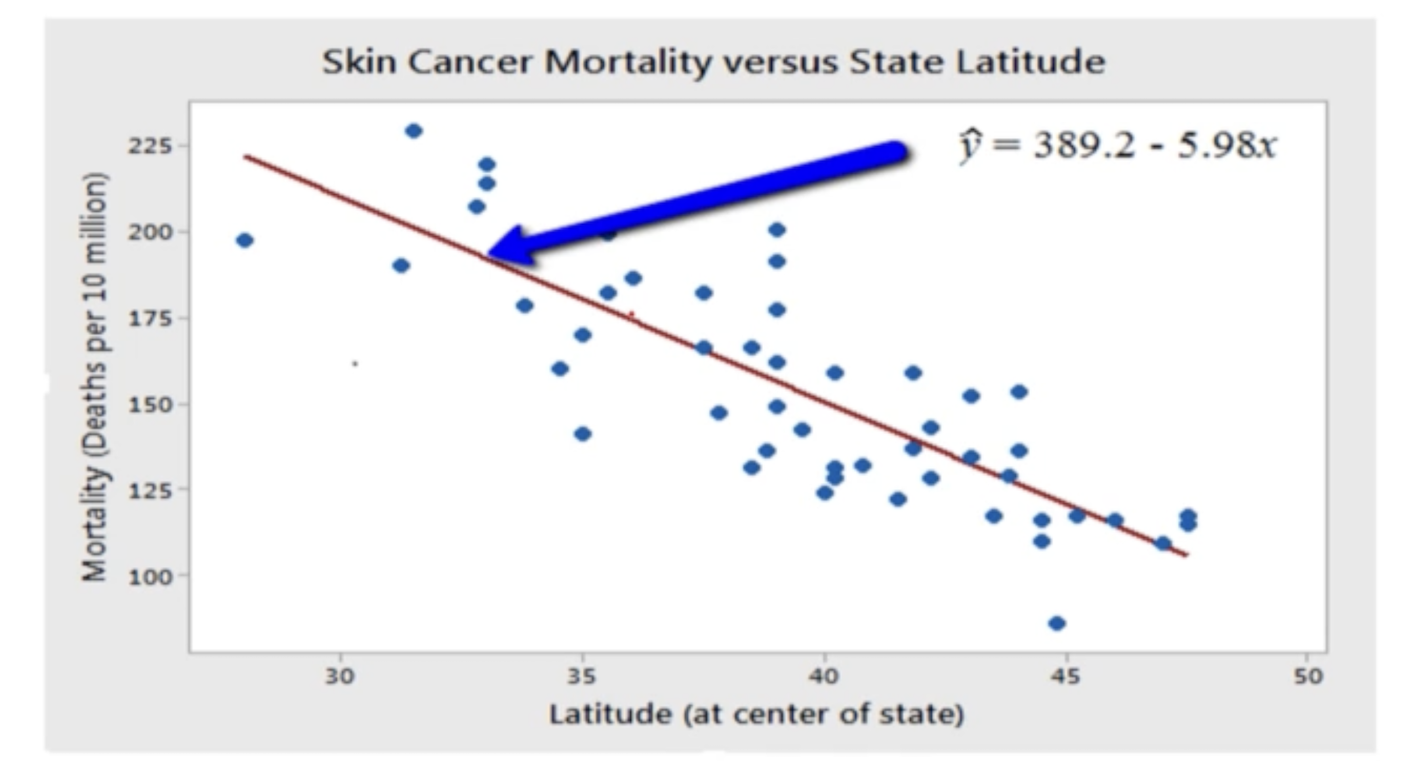
2. Best Fitting Line
1. What is the "Best Fitting Line"?
2. Notation
-\(y_i\): i번째 학생에 대한 관찰된 반응입니다.
-\(x_i\): i번째 학생에 대한 예측 값입니다.
-\(\hat{y_i}\): i번째 학생에 대한 예측된 반응(또는 적합 값)
-실험 단위: 측정이 이루어지는 물체 또는 사람
3. Prediction Error (예측 오차)
- w = -266.5 + 6.1h
- \(x_1\)=63, \(y_1\) =127
- \(\hat{y_1}\)=-266.5 + 6.1 × 63 = 117.8
- 예측 오차(잔여 오차)
- \(e_i\) = \(y_i\) - \(\hat{y_i}\)
- 예: \(y_1\) - \(\hat{y_1}\) =127 - 117.8 = 9.2
4. Least Squares (최소 제곱)
- '가장 잘' 맞는 선은 관찰된 각 데이터 포인트와의 예측 오차를 최소화하는 선입니다. 이를 달성하기 위한 일반적인 방법은 "최소 제곱 기준"을 사용하여 각 데이터 포인트에서 발생하는 예측 오차의 제곱을 최소화하는 것입니다.
■ \( L=\sum_{i=1}^{n}{e_{i}}^{2}=\sum_{i=1}^{n}(y_i -\hat{y_i})^{2}\). -> Loss funtion
- \( \hat{y_i}=b_0 +b_1x_i\)
- \( e_i = y_i-\hat{y_i}\) 데이터 포인트 i에 대한 예측 오차
- \( {e_i}^2 = (y_i -\hat{y_i})^2\): 데이터 포인트 i에 대한 제곱 예측 오차
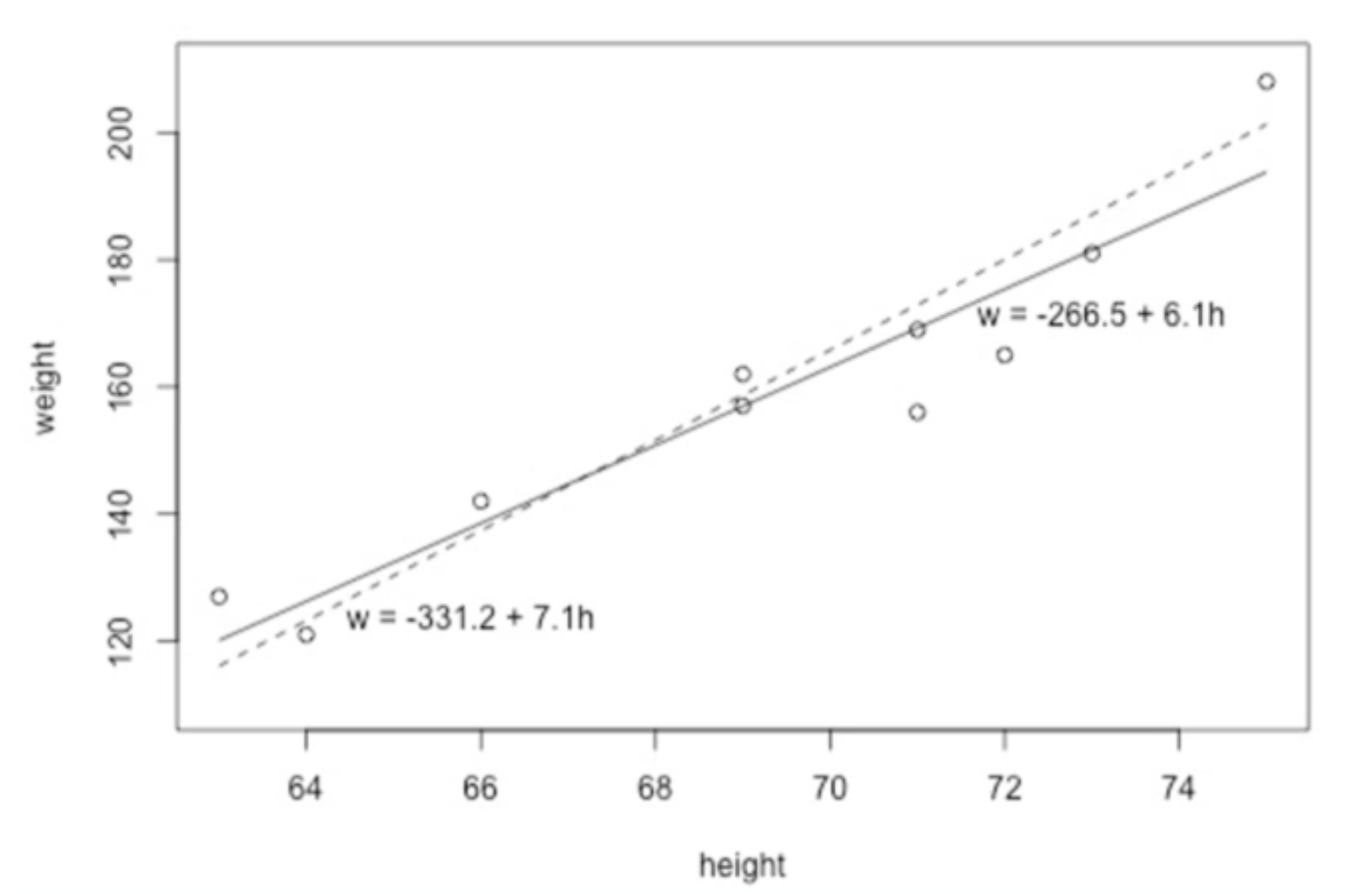
■ 예제
- (실선) w = -266.5 + 6.1h, L = 597.4
- (점선) w = -331.2.5 + 7.1h, L = 766.5
...작성중
3. Simple Linear Regression
1. Introdution
1. Simple Linear Regression
■ A statistical method that allows you to summarize and study the relationship between two continuous (quantitative) variables.
- One variable, denoted X, is considered the predictor, explanatory variable, or independent variable.
- The other variable,denoted Y, is regarded as the response outcome or dependent variable.
(For multiple variables -> Multiple Linear Regression,
For ideal variables -> Generalized Linear Model (GLM))
2. Deterministic Relationship
■ Equations exactly describe the relationship between the two variables
- Circumference =\( \pi \) x diameter
- Ohm's Law: I = \( \frac{V}{r} \)
3. Statistical Relationship
■ The relationship between the variables is not perfect.

2. Best Fitting Line
1. What is the "Best Fitting Line"?

2. Notation
-\(y_i\): the observed response for experimental unit i
-\(x_i\): the predictor value for experimental unit i
-\(\hat{y_i}\): the predicted response (or fitted value) for experimental unit i
-experimental unit: the object or person on which the measurement is made
3. Prediction Error
- w = -266.5 + 6.1h
- \(x_1\)=63, \(y_1\) =127
- \(\hat{y_1}\)=-266.5 + 6.1 × 63 = 117.8
- prediction error (residual error)
- \(e_i\) = \(y_i\) - \(\hat{y_i}\)
- e.g. \(y_1\) - \(\hat{y_1}\) =127 - 117.8 = 9.2
4. Least Squares
- A line that fits the data "best" will be one for which the n prediction errors — one for each observed data point — are as small as possible in some overall sense. One way to achieve this goal is to invoke the "least squares criterion," which says to "minimize the sum of the squared prediction errors."
■ \(L=\sum_{i=1}^{n}{e_{i}}^{2}=\sum_{i=1}^{n}(y_i -\hat{y_i})^{2}\)
- \( \hat{y_i}=b_0 +b_1x_i\)
- \( e_i = y_i-\hat{y_i}\) the prediction error for data point i
- \( {e_i}^2 = (y_i -\hat{y_i})^2\): the squared prediction error for data point i
■ Example
- (the solid line) w = -266.5 + 6.1h, L = 597.4
- (the dashed line) w = -331.2.5 + 7.1h, L = 766.5