728x90
반응형
중앙값(median)
- 관찰값의 개수가 짝수일경우 중앙값이 2개이므로 합산후 2로 나눈다.
- 특이점의 영향을 거의 받지 않는다.
- 분포가 한쪽으로 쏠려 있꺼나, 특이점이 존재하는 데이터를 요약할 떄 주로 사용된다.
사분위수(quartiles)

백분위수(percentile)
p백분위수 : 전체 데이터의 p%가 이 값보다 작거나 같은 값
1사분위수 = 25밴분위수
2사분위수 = 50백분위수 = 중앙값
3사분위수 =75백분위수

다섯 수치요약(five-number summary):
최소값, 1사분위수, 중앙값, 3사분위수, 최댓값
데이터의 중심위치와 퍼진 정도를 모두 파악할 수 있다
상자그림(boxplot)

분포와 요약통계량
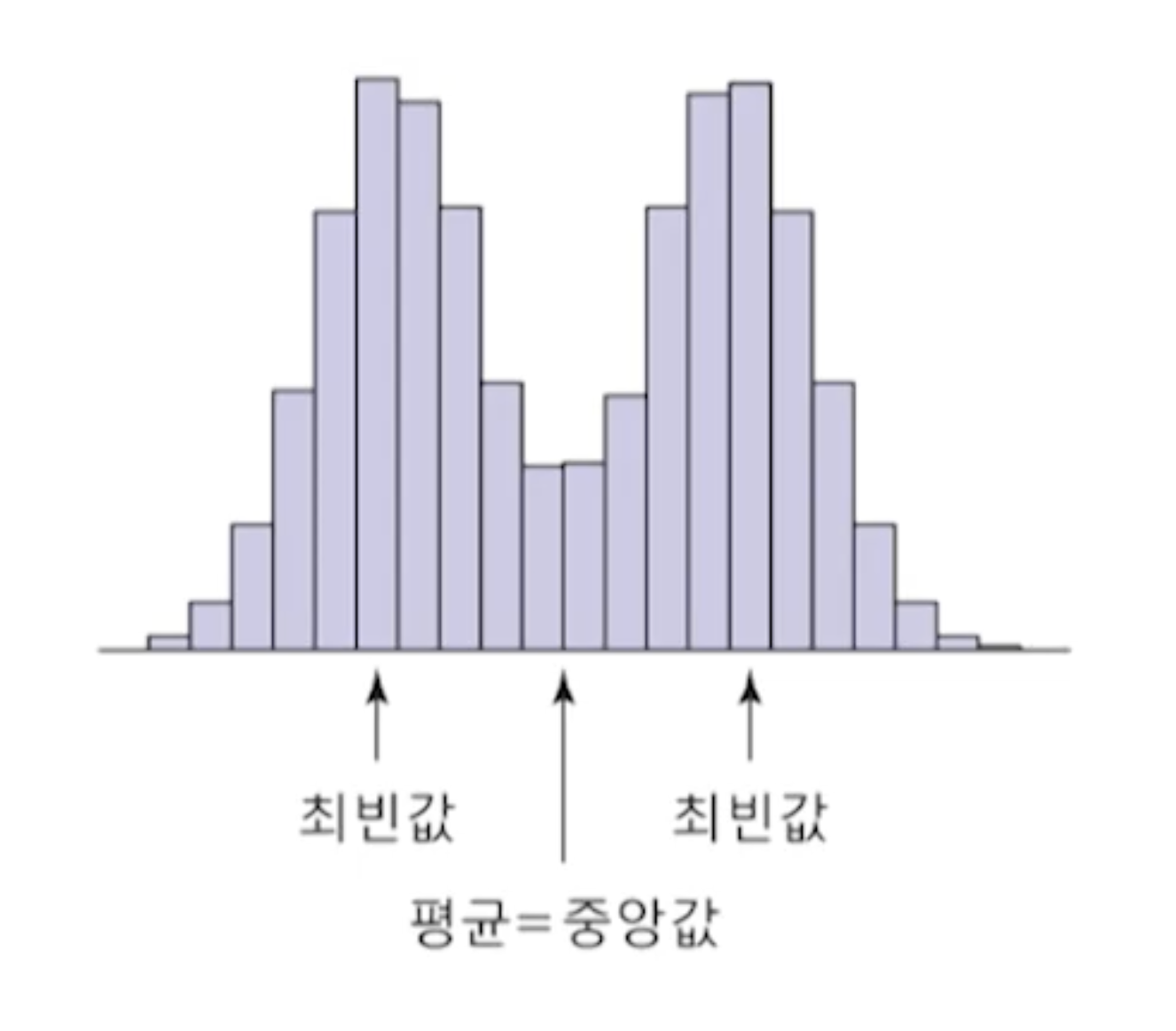
평균: 분포의 무게중심
대칭적인 분포의 경우 데이터를 잘 대표한다
분포가 기울어져 있거나 특이점이 있는 경우 데이터를 잘 대 표하지 못한다
중앙값: 데이터를 크기 순으로 정렬했을 때 가장 가운데에 위치하는 값
분포가 기울어져 있거나 특이점이 있는 경우 많이 쓰인다
최빈값: 빈도가 가장 높은 관찰값
여러개 있을 수도, 하나도 없을 수도 있다
분포의 중심위치에서 멀리 떨어져있을 수도 있다


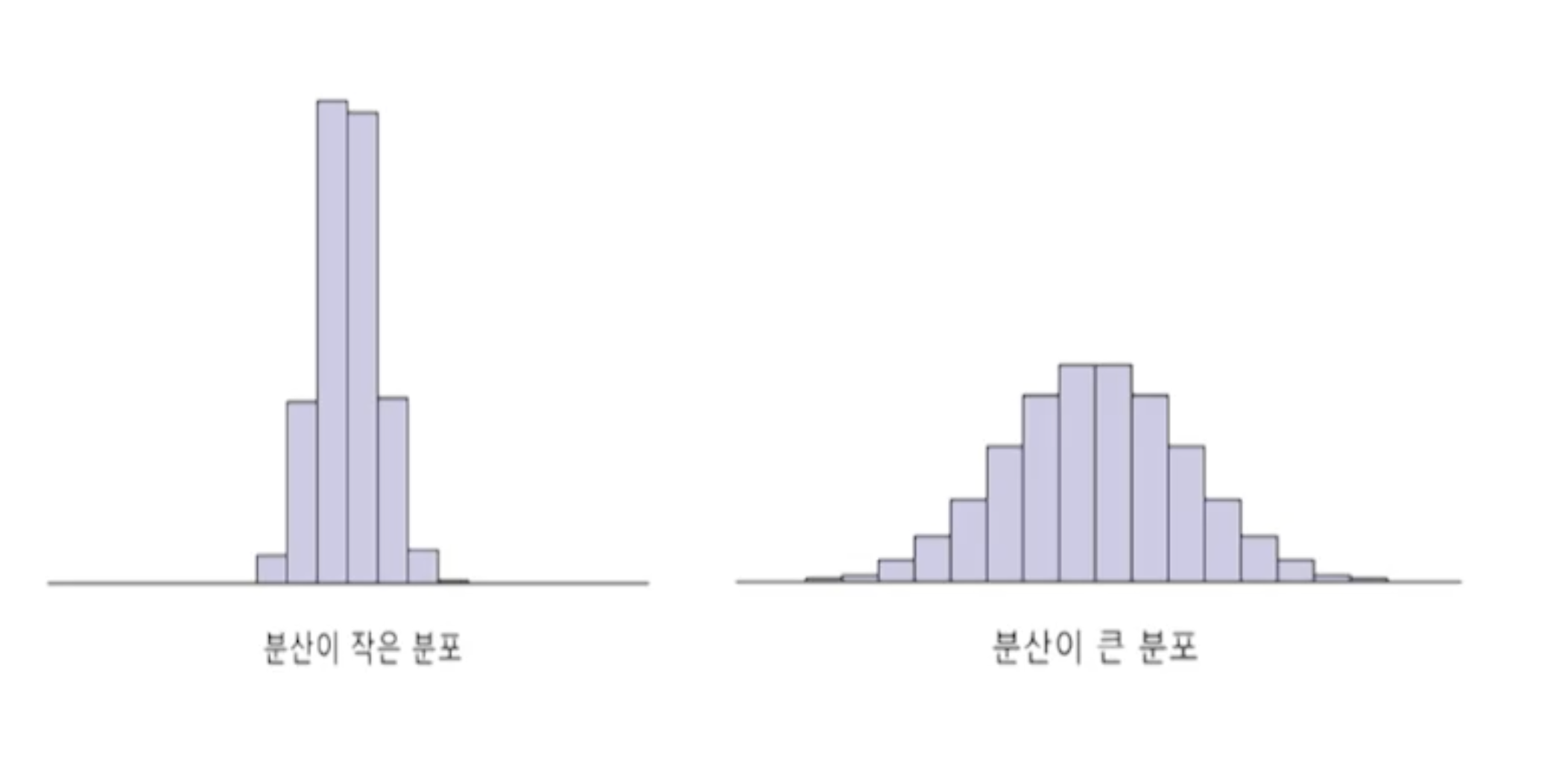
분산: 편차의 제곱의 평균
표준편차: 분산의 제곱근
범위: 최댓값-최솟값
사분위수 범위: 3사분위수-1사분위수
이 값들이 클 수록 데이터의 분포가 많이 퍼진 것이다 분산, 표준편차, 범위는 특이점의 영향을 크게 받는다
사분위수 범위는 특이점에 크게 영향을 받지 않는다
728x90
반응형
'Statistics > [강의정리] 통계학개론' 카테고리의 다른 글
| [통계학개론]03강. R 내장함수 그래프와 요약통계량 (0) | 2024.05.07 |
|---|---|
| [통계학개론] 02강_R 시각화(ggplot2 ) - 막대그래프, 원그래프 (0) | 2024.05.05 |
| [통계학개론] 02강. 데이터 요약1 (1) | 2024.05.05 |
| [통계학개론] 01강. 통계학의 주요 개념 (0) | 2024.05.03 |
| [통계학개론] R기초 (0) | 2024.05.03 |