1. 변수
2. 질적 데이터의 요약-막대그래프
3. 양적 데이터의 요약 - 히스토그램
4. 양적 데이터의 요약-점도표, 평균, 분산
1. 변수
변수의 종류
질적 변수(qualitative variable, 범주형 변수): 유한개 의 범주 중 하나의 값을 취하는 변수 ex) 성별, 학력
양적 변수(quantitative variable): 양적인 수치로 측 정되는 변수 ex) 나이, 몸무게
질적 변수의 종류
명목형 변수(nominal variable): 범주들에 의미 있는 순서 를 정할 수 없는 질적 변수 ex) 성별
순서형 변수(ordinal variable): 범주 간의 의미 있는 순서 를 정할 수 있는 질적 변수 ex) 학력
양적 변수의 종류
연속형 변수(continuous variable): 어떤 실수 구간 안의 모든 값을 가질 수 있는 변수 ex) 몸무게
이산형 변수(discrete variable): 취할 수 있는 값을 셀 수 있는 양적 변 ex) 나이
도수분포표(frequency table)
데이터에서 각 값의 출현빈도나 비슷한 값끼리 묶은 구간별로 관측된 데이터의 개수를 정리한표

도수분포표 만드는법
질적변수 : 각 범주에 속하는 단위의 개수를 제시
양적변수 : 계급을 정한 후 각 계급에 속하는 단위의 개수를 제시
2. 질적 데이터의 요약-막대그래프
명목형 변수: 큰 빈도 -> 작은빈도, 작은빈도 -> 큰빈도 순서로 정렬하면 좋다.
순서형 변수: 범주의 순서를 지켜서 그리는 것이 좋다.
 |
 |
원그래프
막대그래프에 비해서 정보 파악이 어렵기 때문에, 최근에는 선호 되지 않는다.
사견) 가반수 이상이나 특정 데이터의 지배적인 비율을 나태날때 활용하는 경우가 많고 관련해서 유용하다 생각됨.

3. 양적 데이터의 요약 - 히스토그램
도수분포표를 그래프로 나타낸것
계급을 수평축에 표시
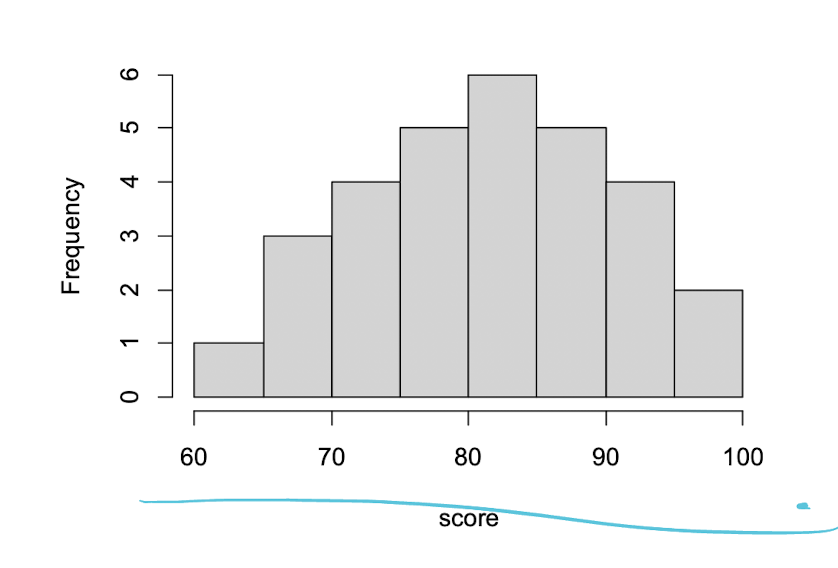
히스토그램을 이용하면 특이점을 쉽게 찾을수 있고
전체적인 분포를 한국에 파악할 수 있다.
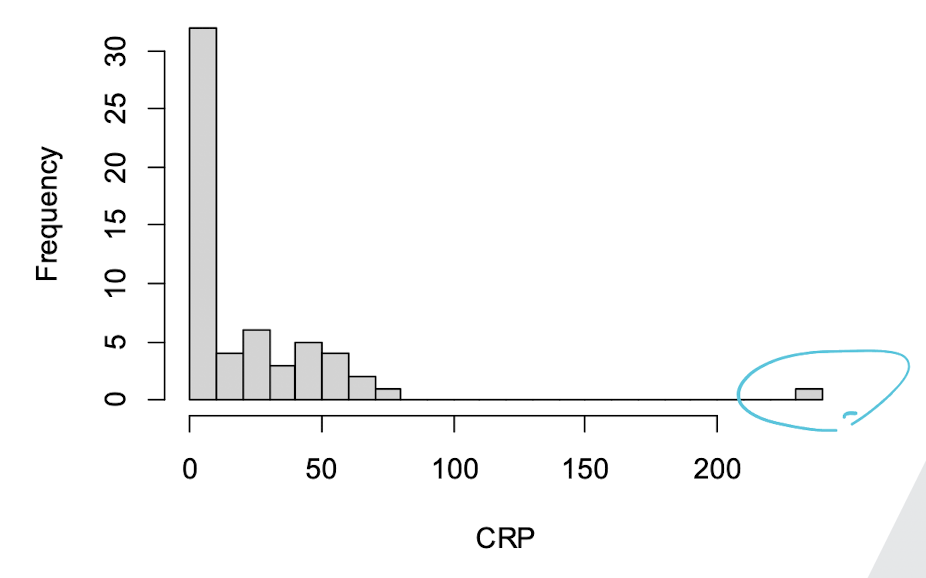
단, 아래의 경우처럼 계급의 폭을 어떻게 하였느냐에 따라서 분포의 특성이 달라보일 수 있다.
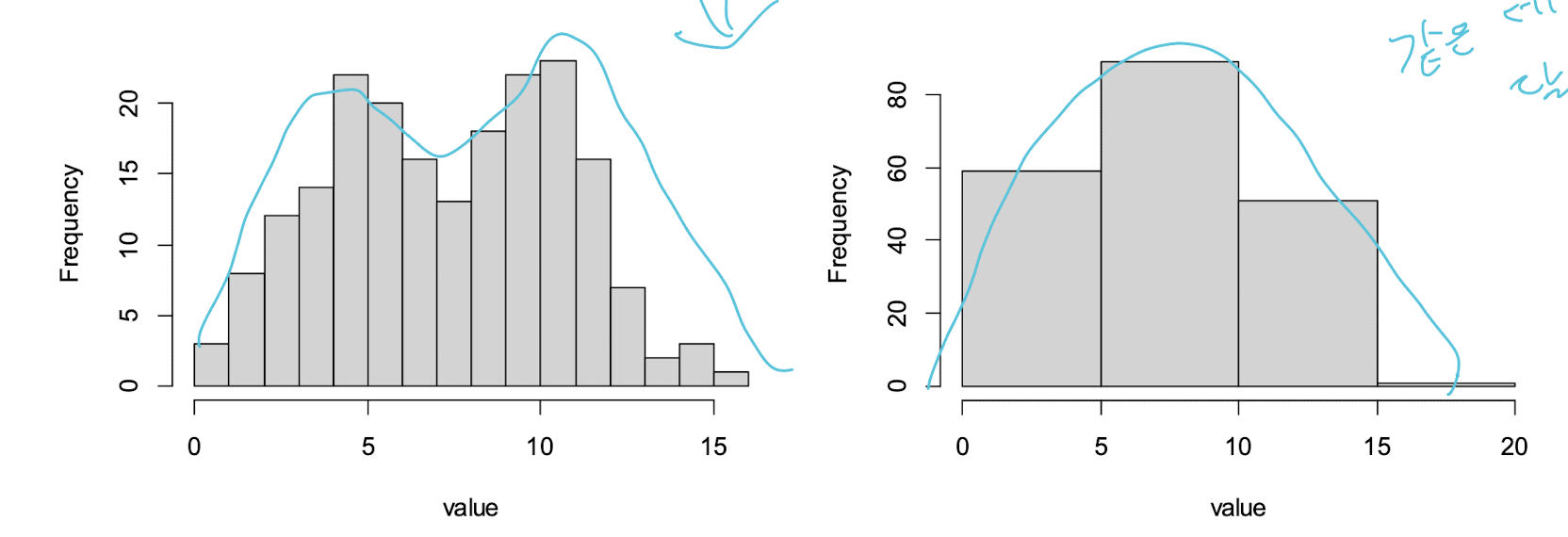
분포의 유형
- 균등분포(uniform distribution) - 일자형태로 고르게 분포
- 종 모양 분포(bell-shaped distribution)
- 쌍봉우리형 분포(bimodal distribution)
-치우친 분포(Skewed distribution): 비대칭으로 한쪽 꼬리가 다른 쪽 꼬리보다 긴 분포.
왼쪽으로 치우친 (right-skewed) 분포: 오른쪽 꼬리가 더 길다.
오른쪽으로 치우친 (left-skewed) 분포: 왼쪽 꼬리가 더 길다.
(영어는 어느쪽에 비스듬한 경사면이 있는가.
왼쪽이 급경사고 오른쪽쪽이 완만한 비스듬한 경사면이면 right-skewed(왼쪽으로치우친)분포)

4. 양적 데이터의 요약-점도표, 평균, 분산
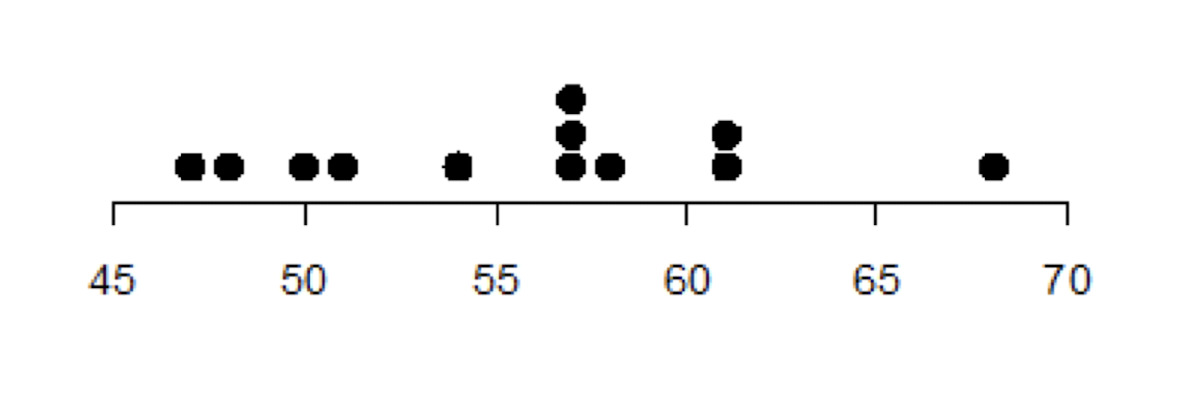
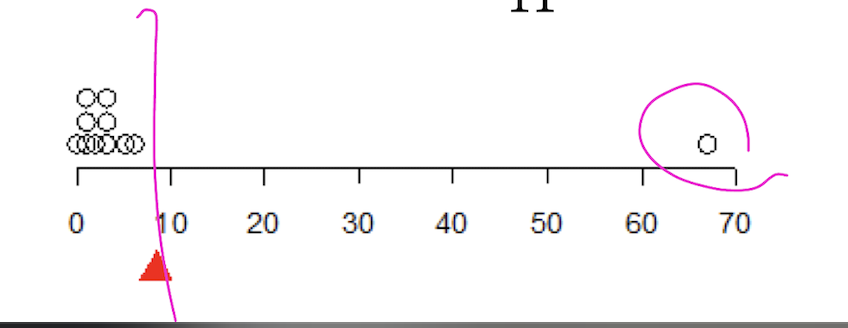
점도표
- 수평선 위에 데이터 값에 해당하는 위치에 점을 찍는 그래프
- 데이터가 작을 때 유용(관찰값의 개수가 20~30개를 넘어가면 너무 복잡해진다.)
평균의 특징
표본데이터가 기울어진 분포를 가졌거나 특이점이 있는 경 우, 평균이 데이터 전체를 잘 대표하지 못한다
특이점의 영향을 크게 받는다
편차; 관찰값 - 평균
분산(variance): 편차의 제곱의 평균
(n으로 나누는 것보다 n-1로 나누는 것이 모분산의 평균에 가깝다.)
표준편차(standard deviatoin): 분산의 제곱근
분산, 표준편차는 특이점의 영향을 많이 받는다.
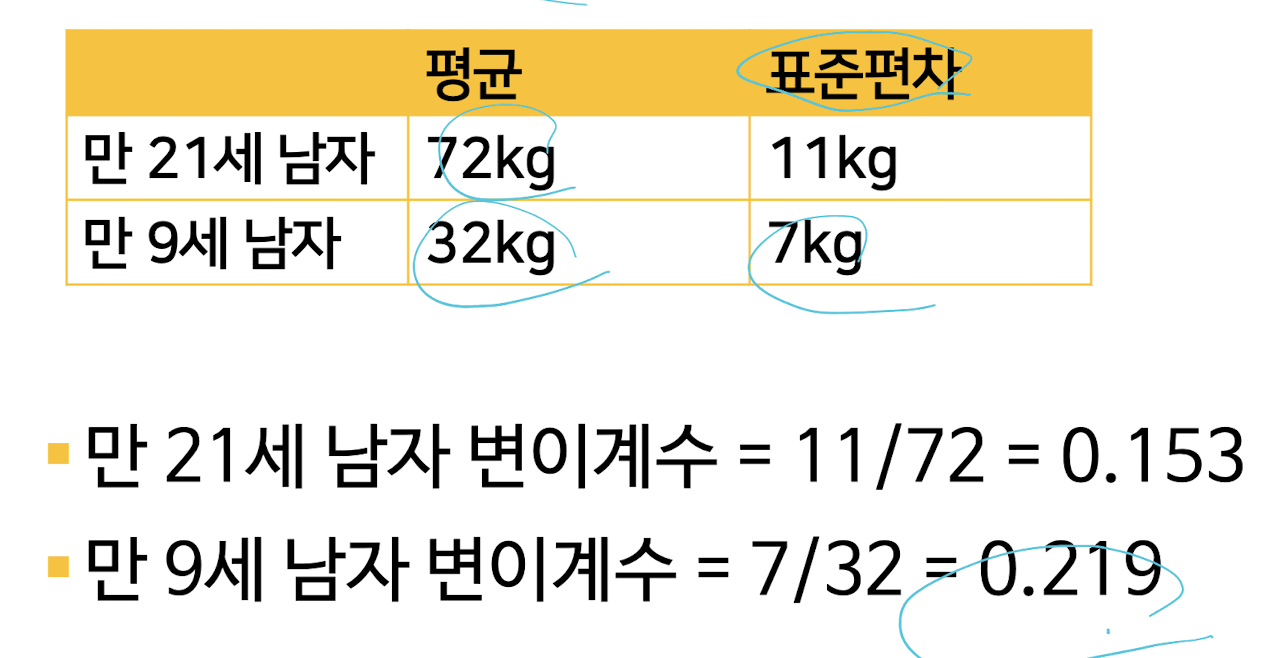
변이계수(coefficient of variation)
변이계수: 표준 편차를 평균으로 나눈 값
'Statistics > [강의정리] 통계학개론' 카테고리의 다른 글
| [통계학개론]03강. R 내장함수 그래프와 요약통계량 (0) | 2024.05.07 |
|---|---|
| [통계학개론] 03강. 데이터요약2 (1) | 2024.05.06 |
| [통계학개론] 02강_R 시각화(ggplot2 ) - 막대그래프, 원그래프 (0) | 2024.05.05 |
| [통계학개론] 01강. 통계학의 주요 개념 (0) | 2024.05.03 |
| [통계학개론] R기초 (0) | 2024.05.03 |