원문
https://table-representation-learning.github.io/assets/papers/tabpfn_a_transformer_that_solv.pdf
한글 번역문
인공지능 기반의 번역기을 이용한 번역이므로 매끄럽지 않을 수 있습니다.
원문과 함께 비교해가며 보시면 빠르게 논문을 리뷰하실 수 있으실것입니다.
Abstract
소규모 데이터 세트에 대해 1초 이내에 표 형식의 지도 분류를 수행할 수 있고, 하이퍼파라미터 튜닝이 필요 없으며, 최첨단 분류 방법과 경쟁할 수 있는 학습된 Transformer 모델인 TabPFN을 소개합니다. TabPFN은 훈련 및 테스트 샘플을 집합값 입력으로 받아들이고 단일 포워드 패스로 전체 테스트 세트에 대한 예측을 산출하는 네트워크의 가중치에 포함된다. TabPFN은 사전 데이터 적합 네트워크(PFN)로, 오프라인에서 한 번만 학습하여 사전에서 추출한 합성 데이터 세트에 대한 베이지안 추론을 근사화합니다. 우리의 선행 데이터에는 인과 학습의 아이디어가 통합되어 있습니다: 여기에는 단순한 구조를 선호하는 구조적 인과 관계 모델의 넓은 공간이 수반됩니다. 그 후, 훈련된 TabPFN은 하이퍼파라미터 튜닝이나 그라데이션 기반 학습 없이 보이지 않는 표 형식의 데이터 세트에 대해 베이지안 예측을 근사화합니다. OpenML-CC18 제품군의 30개 데이터 세트에서 이 방법은 부스트 트리보다 성능이 뛰어나며, 70배 빠른 속도로 복잡한 최신 AutoML 시스템과 동등한 성능을 발휘합니다. GPU를 사용할 수 있는 경우 이 속도는 3,200배로 증가합니다. 유니티의 모든 코드와 훈련된 TabPFN은 https://anonymous.4open.science/ r/TabPFN-2AEE에서 확인할 수 있습니다. https://huggingface. co/spaces/TabPFN/TabPFNPrediction에서 온라인 데모도 제공합니다.
Translated with www.DeepL.com/Translator (free version)
1 Introduction
의료, 금융, 연구, 예측 유지보수 또는 센서 데이터 모델링 분야의 많은 실제 애플리케이션은 표 형식 데이터에 대한 강력한 머신 러닝(ML) 알고리즘에 의존하고 있습니다. 신경망은 많은 ML 작업에서 탁월한 성능을 발휘하지만, 경사 부스트 의사 결정 트리(GBDT, 14)는 짧은 학습 시간과 견고성으로 인해 여전히 표 형식 데이터에 대한 지도 ML의 환경을 지배하고 있습니다[38].
그러나 트리 기반 모델은 차별성이 없기 때문에 딥러닝(DL)에 기반한 다른 블록과 쉽게 구성하고 공동으로 훈련할 수 없습니다. 최근의 많은 연구들이 표 형식 분류를 위한 네이티브 DL 접근법으로 이 문제를 해결하려고 시도하고 있지만[2, 39, 18, 20], 우리는 한 걸음 더 나아가 분류를 스스로 학습하는 트랜스포머[42]를 적용하여 표 형식 데이터 세트에서 DL 모델을 훈련하는 방법과 그로 인해 발생하는 대규모 계산 비용 및 소규모 데이터 세트에서의 과적합 완화 등의 문제를 완전히 우회합니다[18].
Translated with www.DeepL.com/Translator (free version)
우리는 일반적으로 표 형식의 분류가 수행되는 방식에 근본적인 변화를 제안합니다. 새로운 데이터 세트의 학습 부분에 새로운 모델을 처음부터 맞추지 않습니다. 대신, 단순성과 인과적 추론의 원칙을 통합하여 이전의 표 형식 데이터 세트에서 생성된 확률적 분류 작업을 해결하도록 사전 훈련된 대규모 변환기에 대해 단일 포워드 패스를 수행하는 것으로 이 단계를 대체합니다. 이 접근 방식은 표 형식의 분류 작업을 해결하는 시간을 1초 이내로 단축하고, 안정적이고 차별화되며 이식성이 뛰어난 표준 절차인 신경망(NN) 포워드 패스로 적용을 단순화합니다.
이 방법은 훈련 및 예측 알고리즘 자체를 학습하는 사전 데이터 적합 네트워크(PFN, 24, 섹션 2 참조)를 기반으로 합니다. PFN은 베이지안 추론의 근사치를 추정할 수 있는 모든 선행 데이터를 샘플링하여 직접 사후 예측 분포(PPD)를 산출합니다. 따라서 PFN은 선행에 수반되는 데이터에 대한 모든 설명에 암시적으로 가중치를 부여하여 분류 레이블의 확률 분포를 근사화합니다. NN과 GBDT의 귀납적 편향은 L2 정규화, 드롭아웃[40] 또는 제한된 트리 깊이 등을 통해 효율적으로 구현하는 데 의존하는 반면, PFN에서는 원하는 전제를 인코딩하는 데이터 세트 생성 알고리즘을 간단히 설계할 수 있습니다. 이는 학습 알고리즘을 설계하는 방식을 근본적으로 변화시킵니다.
[24]에서는 최대 30개의 훈련 예제만 있고 특징이 거의 없는 매우 작고 균형 잡힌 표 형식의 데이터 세트에 대한 이진 분류 실험을 통해 PFN을 사용한 PPD 근사치를 입증했습니다. 이 작업을 기반으로 최대 1,000개의 훈련 샘플, 100개의 특징, 10개의 클래스로 구성된 혼합 특징 유형, 누락된 데이터, 불균형 타깃으로 구성된 실제 데이터 세트에서 평가하는 표 형식 다중 클래스 분류 작업을 위한 최첨단 모델을 개발했습니다. 소규모 데이터 세트에 초점을 맞춘 이유는 (1) 소규모 데이터 세트는 실제 애플리케이션에서 자주 발생하고, (2) 기존 DL 방법은 이 영역에서 가장 제한적이며, (3) 부록 A에 자세히 설명된 대로 대규모 데이터 세트에 대해 TabPFN을 평가하는 데 훨씬 더 비용이 많이 들기 때문입니다.
우리는 표 형식 데이터의 기초가 되는 복잡한 피처 종속성과 잠재적 인과 메커니즘을 모델링하기 위해 베이지안 신경망(BNN; Neal 26, Gal 15) 및 구조적 인과 모델(SCM; Pearl 27, Peters 외. 31)을 기반으로 선행(섹션 3 참조)을 설계합니다. 우리의 이전 작업은 또한 단순한 SCM과 BNN에 기반한 설명이 더 가능성이 높다는 Occam의 면도날에서 아이디어를 가져옵니다. 선행에서는 데이터 생성 SCM의 평균 노드 수에 대한 로그 스케일 균등 분포와 같은 확률 분포를 통해 선행의 가설을 설명하는 하이퍼파라미터를 정의합니다. 결과 PPD는 이러한 하이퍼파라미터에 대한 불확실성을 암시적으로 모델링하여 데이터 설명에서 하이퍼파라미터에 데이터와 사전 확률이 주어질 가능성에 따라 가중치를 부여합니다. 따라서 PPD를 구하는 것은 단일 포워드 패스에서 무한히 큰 하이퍼파라미터 앙상블(즉, SCM과 BNN의 인스턴스화)에 해당하며 교차 검증이나 모델 선택이 필요하지 않습니다.
마지막으로, 섹션 4에서는 다양한 작업에서 TabPFN의 성능과 동작을 분석하고 소규모 데이터 세트에서 표 형식 분류를 위한 이전 접근 방식과 비교합니다. 정량적으로 볼 때, XGBoost [6], LightGBM [19], CatBoost [32]를 통한 그라데이션 부스팅과 같은 개별 "기본 수준" 분류 알고리즘보다 훨씬 우수한 성능을 제공하며, 단 1초 만에 최고의 AutoML 프레임워크 [8, 11]가 5~30분 내에 달성하는 것과 경쟁할 수 있는 성능을 제공합니다.
2 Background on Prior-Data Fitted Networks
먼저 PFN이 어떻게 작동하는지에 대해 간략하게 요약하고 자세한 내용은 [24]를 참조하세요.
지도 학습을 위한 사후 예측 분포 지도 학습을 위한 베이지안 프레임워크에서, 선행은 일련의 입력 x와 출력 레이블 y의 관계에 대한 가설 Φ의 공간을 정의합니다. 각 가설 φ는 데이터 집합을 구성하는 샘플을 추출할 수 있는 데이터 분포를 생성하는 메커니즘으로 볼 수 있습니다. 예를 들어 구조적 인과 관계 모델에 기반한 선행이 주어졌을 때, Φ는 구조적 인과 관계 모델의 공간이고, 가설 φ는 특정 SCM 하나이며, 데이터 세트는 SCM을 통해 생성된 샘플로 구성됩니다. 실제로 데이터 세트는 관찰된 레이블이 있는 학습 데이터와 예측 성능을 평가하기 위해 레이블이 누락되거나 보류된 테스트 데이터로 구성됩니다. 테스트 샘플 xtest에 대한 PPD는 훈련 샘플 세트 Dtrain := {(x1, y1), . . . , (xn, yn)}이며 해당 레이블 p(-|xtest, Dtrain)의 분포를 지정합니다. 이 값은 가설 Φ의 공간에 대한 적분으로 구할 수 있으며,

여기서 가설의 가중치는 그림 1: 왼쪽 (a)입니다: 훈련 샘플 {(x1, y1), .. . , (x3, y3)}는 3개의 토큰으로 변환되어 서로에게 영향을 미치며, 테스트 샘플 x4와 x5는 훈련 샘플에만 영향을 미칩니다. 오른쪽 (b): PFN은 오프라인 단계에서 주어진 선행의 PPD를 근사화하여 온라인 단계에서 단 한 번의 포워드 패스로 새로운 데이터 세트에 대한 예측을 생성하는 방법을 학습합니다. 24]를 기반으로 한 플롯.
사전 확률과 이 가설이 주어진 관측의 가능성에 따라 결정됩니다:

일반적으로 PPD를 구하는 것은 어렵지만, 샘플을 구할 수 있는 모든 선행 데이터를 고려할 때 PFN은 PPD를 근사화합니다. 훈련 목표를 글로벌 최소값으로 최소화하는 PFN은 [24]에서 볼 수 있듯이 PPD에 정확히 근사치를 구할 수 있습니다.
아키텍처 PFN은 각 특징 벡터와 레이블을 토큰으로 인코딩하는 트랜스포머[42]에 의존하며, 그림 1a에 표시된 것처럼 토큰 표현이 서로를 참조할 수 있도록 합니다. 이들은 특징 벡터와 라벨 벡터의 가변 길이 훈련 세트 Dtrain과 특징 벡터에 대한 가변 길이 쿼리 세트 xtest ={x(test,1),...,x(test,m)} 및 각 쿼리에 대한 PPD의 추정치를 받아들입니다.
합성 사전 피팅 사전 피팅 중에 PFN은 사전 샘플링 체계 p(D) = Eφ∼p(φ)[p(D|φ)]로 지정된 사전이 주어지면 베이지안 추론을 근사화하도록 훈련되며, 먼저 φ ∼ p(φ)로 가설(생성 메커니즘)을 샘플링한 다음 D ∼ p(D|φ)로 합성 데이터 세트를 샘플링합니다. 이러한 합성 데이터 세트 D := (xi, yi)i∈{0,...,n}을 반복적으로 샘플링하고 PFN의 파라미터 θ를 최적화하여 홀드아웃 레이블 ytest가 있고 나머지 데이터 세트 Dtrain = D \ Dtest에 조건부로 지정된 Dtest ⊂ D에 대한 예측을 수행합니다. 이렇게 하면 근사화된 PPD qθ에 대한 샘플링된 데이터 세트에 대한 교차 엔트로피 손실이 최소화됩니다:

24]에서 입증된 바와 같이, 이 손실을 최소화하면 정확한 베이지안 사후 예측에 근접하게 됩니다. 그림 1b에서 이를 시각화하고 부록의 알고리즘 1에서 전체 훈련 설정을 자세히 설명합니다. 결정적으로, 이 합성 사전 적합 단계는 주어진 사전 p(D)에 대해 단 한 번만 수행되며, 새로운 데이터 세트에 대해 실제 세계 추론을 수행하는 방법을 학습합니다.
실제 세계 추론 추론 중에 훈련된 모델은 임의의 실제 세계 데이터 세트에 적용됩니다. 훈련 샘플 Dtrain과 테스트 특징 xtest가 있는 새로운 데이터 세트의 경우, 이를 위에서 훈련된 모델에 입력으로 제공하면 단일 포워드 패스에서 PPD qθ(y|xtest,Dtrain)가 산출됩니다. 그런 다음 PPD 클래스 확률을 실제 작업에 대한 예측으로 사용합니다. 따라서 PFN은 훈련과 예측을 한 번에 수행하며(가우시안 프로세스를 사용한 예측과 유사), 새로운 데이터 세트를 예측할 때 경사 기반 학습을 사용하지 않습니다.
3 A Prior for Tabular Data
이 방법의 성능은 적합한 선행의 사양에 따라 결정적으로 달라지는데, PFN은 이 선행의 PPD를 근사화하기 때문입니다. 3.1절에서는 선행의 거의 모든 하이퍼파라미터에 대해 점 추정치 대신 분포를 사용하는 기본 기법에 대해 간략히 설명합니다. 3.2절에서는 예측의 단순화에 대한 동기를 부여하고, 3.3절과 3.4절에서는 예측에서 다양한 데이터를 생성하는 기본 메커니즘으로 구조적 인과 모델(SCM)과 베이지안 신경망(BNN)을 사용하는 방법을 설명합니다. SCM과 BNN 전제는 회귀 작업만 생성하므로, 3.5절에서 이를 분류 작업으로 변환하는 방법을 보여드리겠습니다. 표 형식의 데이터를 더 잘 반영하기 위해 선행에 대한 추가적인 개선 사항은 부록 D.2에서 설명합니다.

3.1 Fundamentally Probabilistic Models
모델을 맞추려면 일반적으로 임베딩 크기, 레이어 수, NN의 활성화 함수 등 적합한 하이퍼파라미터를 찾아야 합니다. 일반적으로 적합한 하이퍼파라미터를 찾기 위해 리소스 집약적인 검색을 사용해야 합니다[23, 50, 9]. 하지만 이러한 검색의 결과는 하이퍼파라미터 선택에 대한 점 추정치일 뿐입니다. 여러 아키텍처와 하이퍼파라미터 설정을 조합하면 이러한 하이퍼파라미터에 대한 분포에 대한 대략적인 근사치를 얻을 수 있으며 성능이 향상되는 것으로 나타났습니다[48, 44]. 그러나 이 방법은 고려되는 선택의 수에 따라 비용이 선형적으로 확장됩니다.
PFN을 사용하면 단일 포워드 패스에서 모델의 하이퍼파라미터에 대해 완전한 베이지안 방식을 사용할 수 있습니다. BNN 아키텍처와 같이 이전의 하이퍼파라미터 공간에 대한 확률을 정의함으로써 TabPFN에 의해 근사화된 PPD는 이 하이퍼파라미터 공간과 각 모델 가중치에 대해 공동으로 통합됩니다. 이 접근 방식을 하이퍼파라미터뿐만 아니라 서로 다른 전제 조건에 대한 혼합으로 확장하여 BNN과 SCM 전제를 혼합하고, 각 전제 조건은 다시 아키텍처와 하이퍼파라미터의 혼합을 수반합니다.
3.2 Simplicity
트위터에서는 오캄의 면도기나 스피드 프라이어[35]와 같은 단순성 개념에 기초하여 프라이어를 결정합니다. 경쟁 가설을 고려할 때는 더 간단한 가설, 예를 들어 더 적은 수의 매개변수를 필요로 하는 가설을 선호합니다. 그러나 단순성의 개념은 단순성을 정의하는 특정 기준을 선택하는 데 달려 있습니다. 다음에서는 단순성이 노드와 매개변수가 적은 그래프로 구체화되는 SCM과 BNN을 기반으로 하는 선행을 소개합니다.
3.3 Structural Causal Prior
인과 지식은 반지도 학습, 전이 학습, 분포 외 일반화 등 다양한 ML 작업을 용이하게 할 수 있음이 입증되었습니다 [37, 17, 34]. 표 형식의 데이터는 종종 열 간의 인과 관계를 나타내며, 인과 메커니즘은 인간의 추론에서 강력한 선행 요소로 밝혀졌습니다 [43, 45]. 따라서 우리는 인과 관계를 모델링하는 SCM을 기반으로 TabPFN을 선행합니다[27, 31]. SCM은 구조적 할당(메커니즘이라고 함)의 컬렉션 Z := ({z1 , . . . , zk })로 구성됩니다.

여기서 PAg (i)는 기본 DAG G(인과 그래프)에서 zi(직접 원인)의 부모 집합이고, fi는 (잠재적으로 비선형적인) 결정론적 함수이며, εi는 잡음 변수입니다. G의 인과 관계는 그림 2에 시각화된 것처럼 원인에서 결과를 가리키는 방향 에지로 표현되며, 각 메커니즘 zi는 G의 노드에 할당됩니다.
이전 작업과의 관계 인과적 추론을 예측에 통합하는 방법에는 인과적 추론과 인과적 발견이라는 두 가지 주요 방법이 있습니다. 여기에서는 이 두 가지 방법을 간략하게 설명하고, 두 접근 방식이 어떻게 다른지 설명합니다. 인과 추론은 개입과 관찰 데이터를 사용하여 시스템 구성 요소 간의 인과 관계를 파악하고자 합니다[28].

인과적 발견은 순수하게 관찰 데이터를 분석하여 인과적 정보를 밝히고자 합니다[49]. 이러한 인과적 표현은 새로운 샘플에 대한 예측을 하거나 설명 가능성을 제공하는 데 사용됩니다. 대부분의 기존 연구는 다운스트림 예측에 사용할 단일 인과 그래프를 결정하는 데 중점을 둡니다. 이는 대부분의 종류의 SCM이 개입 데이터 없이는 식별할 수 없고, DAG 공간의 조합적 특성으로 인해 호환 가능한 DAG의 수가 폭발적으로 증가하기 때문에 문제가 될 수 있습니다. 1]은 이러한 표현을 이산 DAG의 공간으로 확장했지만, 이 작업은 계산 복잡도가 높은 반면 SCM의 몇 가지 하위 계열로 제한됩니다. TabPFN은 단일 포워드 패스에서 전체 가설 공간, 즉 광범위한 SCM 제품군과 각각의 가중치를 효과적으로 추론합니다. 이를 위해 추론 단계에서 명시적인 그래프 표현을 생략하고 PPD를 직접 근사화합니다. 따라서 인과 관계 추론이나 발견을 수행하지 않고 다운스트림 예측 작업을 직접 해결합니다. 이러한 암묵적인 인과관계 가정을 사용하는 것은 추론 범주를 추상화한 Pearl의 "인과관계 사다리"로 설명할 수 있는데, 각 높은 사다리는 추론과 관련된 개념이 더 많음을 나타냅니다[29]. 가장 낮은 단계에는 ML의 대부분을 포함하는 연관성이 있습니다. 두 번째 단계에서는 개입의 효과를 예측하는 것, 즉 기능에 직접적으로 영향을 미칠 때 어떤 일이 일어나는지 예측하는 것입니다. 우리의 작업은 [21, 22]와 유사한 "1.5단계"로 간주할 수 있습니다. 개입의 효과를 예측하려는 것이 아니라 인과적 메커니즘이 데이터를 생성한다는 가정을 사용하여 관찰 데이터에 대해 보다 정보에 입각한 예측을 수행하기 때문입니다.
순수한 관찰 데이터[49]를 분석하여 인과관계를 도출합니다. 이러한 인과 관계 표현은 새로운 샘플에 대한 예측을 하거나 설명 가능성을 제공하는 데 사용됩니다. 대부분의 기존 연구는 다운스트림 예측에 사용할 단일 인과 그래프를 결정하는 데 중점을 둡니다. 이는 대부분의 종류의 SCM이 개입 데이터 없이는 식별할 수 없고, DAG 공간의 조합적 특성으로 인해 호환 가능한 DAG의 수가 폭발적으로 증가하기 때문에 문제가 될 수 있습니다. 1]은 이러한 표현을 이산 DAG의 공간으로 확장했지만, 이 작업은 계산 복잡도가 높은 반면 SCM의 몇 가지 하위 계열로 제한됩니다. TabPFN은 단일 포워드 패스에서 전체 가설 공간, 즉 광범위한 SCM 제품군과 각각의 가중치를 효과적으로 추론합니다. 이를 위해 추론 단계에서 명시적인 그래프 표현을 생략하고 PPD를 직접 근사화합니다. 따라서 인과 관계 추론이나 발견을 수행하지 않고 다운스트림 예측 작업을 직접 해결합니다. 이러한 암묵적인 인과관계 가정을 사용하는 것은 추론 범주를 추상화한 Pearl의 "인과관계 사다리"로 설명할 수 있는데, 각 높은 사다리는 추론과 관련된 개념이 더 많음을 나타냅니다[29]. 가장 낮은 단계에는 ML의 대부분을 포함하는 연관성이 있습니다. 두 번째 단계에서는 개입의 효과를 예측하는 것, 즉 기능에 직접적으로 영향을 미칠 때 어떤 일이 일어나는지 예측하는 것입니다. 우리의 작업은 [21, 22]와 유사한 "1.5단계"로 간주할 수 있습니다. 개입의 효과를 예측하려는 것이 아니라 인과적 메커니즘이 데이터를 생성한다는 가정을 사용하여 관찰 데이터에 대해 보다 정보에 입각한 예측을 수행하기 때문입니다.
Method SCM을 기반으로 PFN 전제를 생성하려면 지도 학습 작업(즉, 데이터 세트)의 샘플링 절차를 정의해야 합니다. 여기서 각 데이터 세트는 무작위로 샘플링된 하나의 SCM(유도 DAG 구조, 활성화 함수, 결정론적 함수 fi)을 기반으로 합니다. SCM이 주어지면 합성 데이터 세트의 각 피처에 대해 하나씩 G의 노드 집합 zX와 인과 그래프 G의 노드 zy를 샘플링합니다. 이러한 노드는 관찰 노드로서, zX의 값은 피처 집합에 포함되고 zy의 값은 타깃으로 작용하게 됩니다. 이러한 각 SCM과 노드 목록 zX 및 zy에 대해 SCM의 모든 노이즈 변수를 n번 샘플링하고 그래프를 통해 전파하여 n개의 샘플을 생성하고 모든 인스턴스에 대해 zX 및 zy 값을 검색합니다. 그림 2는 관찰된 특징 노드와 대상 노드가 회색으로 표시된 SCM을 보여줍니다. 그림 3b는 두 개의 서로 다른 SCM에서 생성된 샘플의 산점도를 보여줍니다. 생성된 특징과 표적은 생성된 DAG 구조를 통해 상호 연관됩니다. 이는 전후 인과 관계를 통해 조건부 종속적 특징, 즉 타깃이 특징의 원인 또는 결과일 수 있는 특징으로 이어집니다.
이 작업에서는 부록 D.1에 설명된 대로 효율적으로 샘플링할 수 있는 DAG와 결정론적 함수 fi의 서브패밀리를 인스턴스화합니다. 그리고 SCM을 효율적으로 샘플링하는 것이 우리가 가진 유일한 재검증이기 때문에, 인스턴스화된 서브패밀리는 여러 활성화 함수와 잠재적으로 비 가우시안 노이즈를 포함하여 매우 일반적입니다.
PPD를 설명하는 방정식 1로 돌아가면 다음과 같이 이전 SCM의 맥락에서 이해할 수 있습니다: PPD는 SCM 그래프 가설의 공간에 대한 예측을 통합하며, 각 가설의 가중치는 이 가설이 주어진 데이터를 관찰할 가능성과 선행에서 이 가설의 가능성에 의해 결정됩니다.
3.4 BNN Prio
또한 뮐러 등[24]이 소개한 BNN 선행을 고려하고, PFN 훈련 중에 둘 중 하나 또는 다른 선행에서 데이터 세트를 무작위로 샘플링하여 위에서 설명한 SCM 선행과 혼합합니다(하이퍼파라미터 샘플 SCM 대 BNN으로 가중치 부여, 부록 F.4 참조). BNN 선행에서 데이터 세트를 샘플링하려면 먼저 NN 아키텍처와 그 가중치를 샘플링합니다. 그런 다음 생성될 데이터 세트의 각 데이터 포인트에 대해 입력을 샘플링하고, 샘플링된 노이즈 변수와 함께 BNN을 통해 입력 x를 공급하고 출력 y를 타겟으로 사용합니다(그림 2 참조). 이는 표준 BNN보다 더 일반적인 설정으로, 후행은 고정 아키텍처의 가중치에 대한 표준 분포뿐만 아니라 아키텍처에 대한 분포도 고려하기 때문입니다. 이 접근 방식에 대한 자세한 내용은 Müller 등[24]의 선행 연구에서 확인할 수 있습니다.
3.5 Multi-class Prediction
지금까지 설명한 선구자들은 스칼라 레이블을 반환합니다. 합성 분류 레이블을 생성하려면 스칼라 레이블 yˆ를 이산형 클래스 레이블 y로 변환해야 합니다. 이를 위해 yˆ의 값을 클래스 레이블에 매핑되는 간격으로 간단히 분할하면 됩니다:
1. 클래스 수 Nc ∼ p(Nc)를 샘플링합니다. 여기서 p(Nc)는 정수에 대한 분포입니다. 2. Nc - 1 바운드 Bc ∼ p(Bc|Nc, yˆ)를 샘플링합니다. 여기서 p(Bc|Nc, yˆ)는 yˆ에서 임의의 값(
를 샘플링합니다.
3. 각 스칼라 레이블 yˆi를 그것을 포함하는 비열한 간격의 인덱스에 매핑합니다: yi ←.
Pj[Bj < yˆi], 여기서 [-]는 지표 함수입니다.
예를 들어, Nc = 3 클래스인 경우 경계 Bc = {-0.1, 0.5}는 세 개의 구간 {(-∞, -0.1], (-0.1, 0.5], (0.5, ∞)}을 정의합니다. 모든 yˆi는 -0.1보다 작으면 레이블 0에, (-0.1, 0.5]에 있으면 1에, 그 외에는 2에 매핑됩니다. 마지막으로 클래스의 레이블을 섞습니다. 즉, 범위에 따라 클래스 레이블의 순서를 제거합니다.
4 Experiments
4.1 Evaluation on Toy Problems
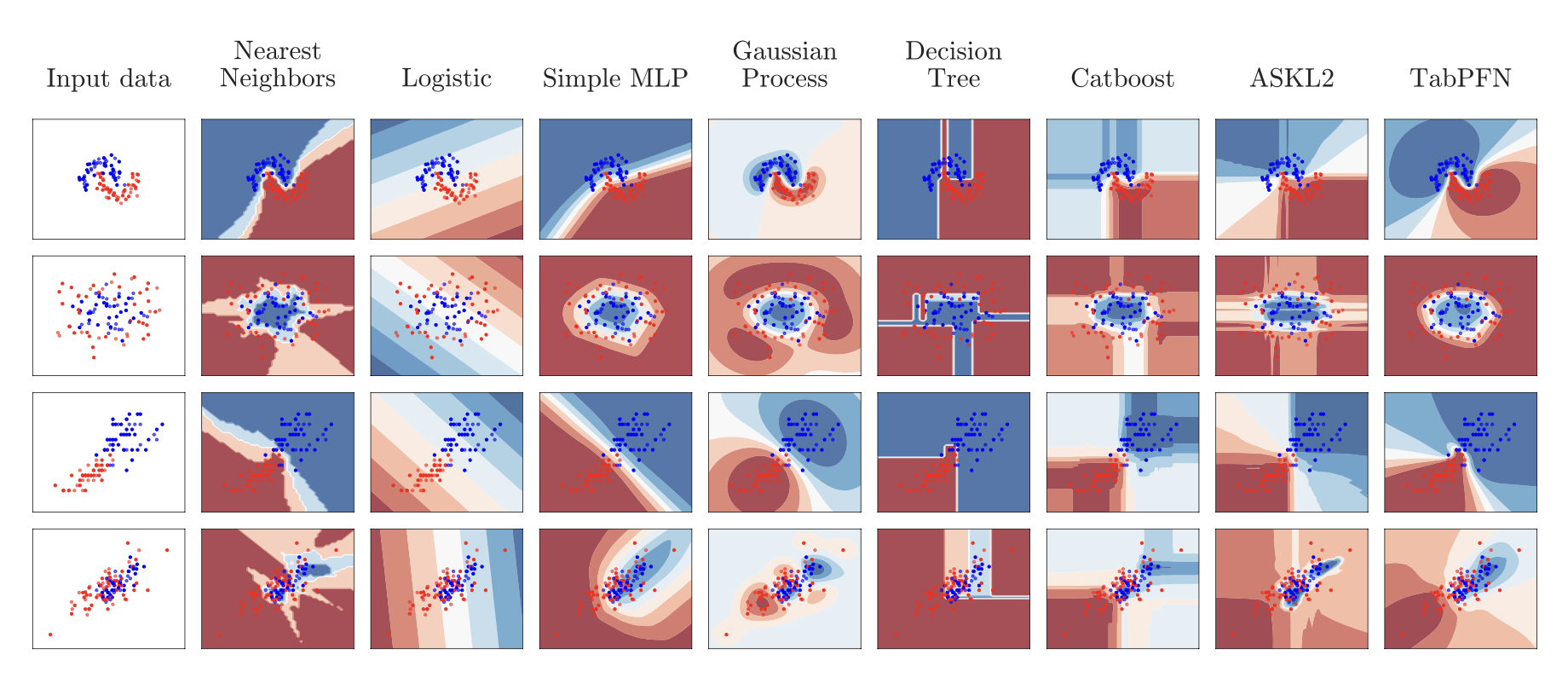
그림 4에서 하이퍼파라미터 튜닝을 하지 않은 표준 분류기와 TabPFN을 정성적으로 비교합니다. 맨 위 줄은 노이즈가 있는 달 데이터 세트를 보여줍니다. TabPFN은 샘플 간의 결정 경계를 정확하게 모델링하며, 가우시안 프로세스와 마찬가지로 관측된 샘플에서 멀리 떨어진 지점의 경우 불확실성이 큽니다. 두 번째 행은 노이즈가 있는 원 데이터 집합을 보여줍니다: TabPFN은 샘플이 혼합된 영역을 벗어난 곳에서는 높은 신뢰도로 원의 모양을 정확하게 모델링합니다. 세 번째 행은 홍채 데이터 세트의 두 가지 클래스와 특징을, 네 번째 행은 와인 데이터 세트의 두 가지 클래스와 특징(둘 다 scikit-learn에 포함됨)을 보여줍니다.

4.2 Evaluation on Tabular AutoML Tasks
이제 실제 분류 작업에 대한 경험적 분석으로 넘어갑니다. 표 형식 분류를 위한 최첨단 ML 및 AutoML 방법과 우리의 방법을 비교합니다.
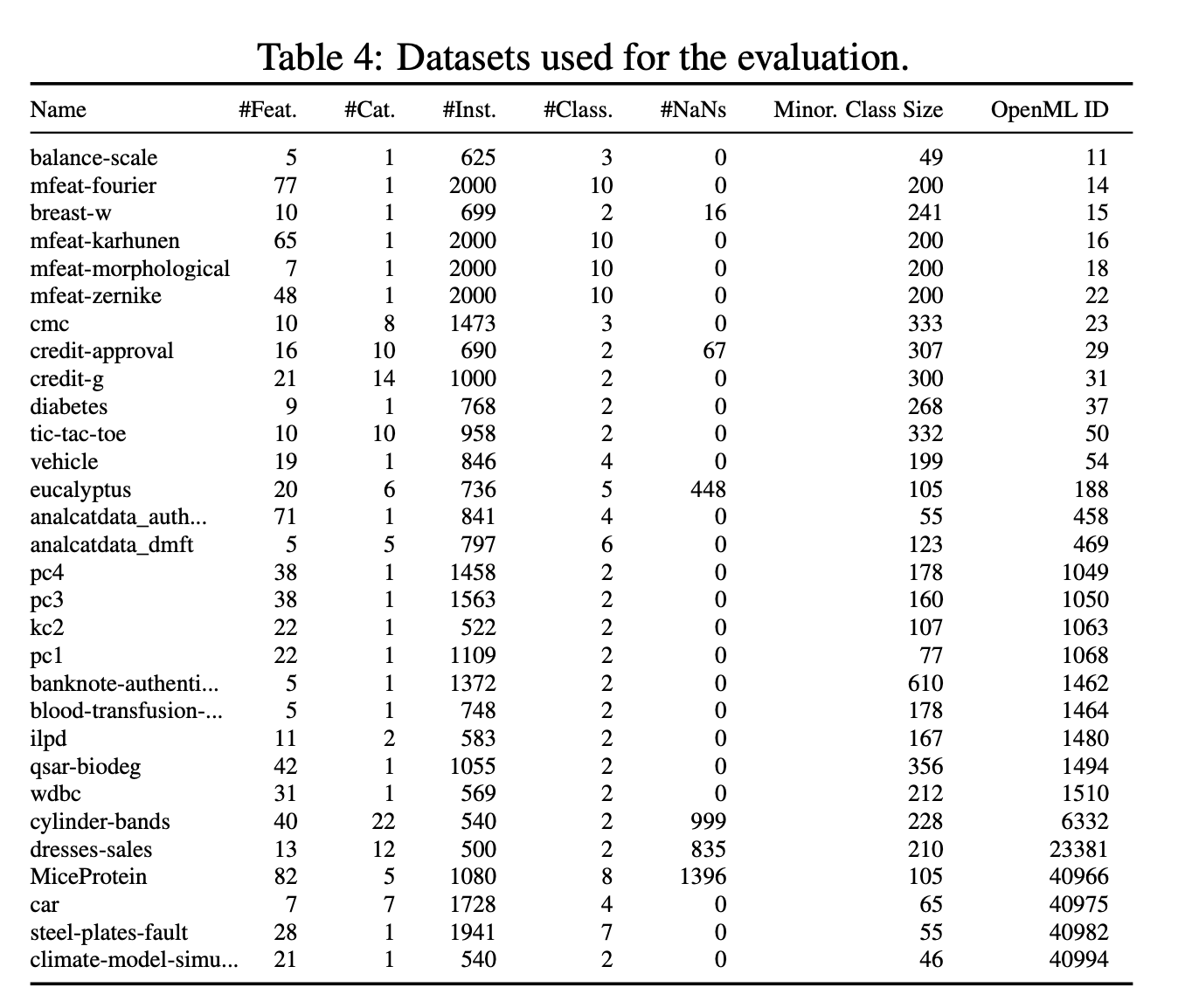
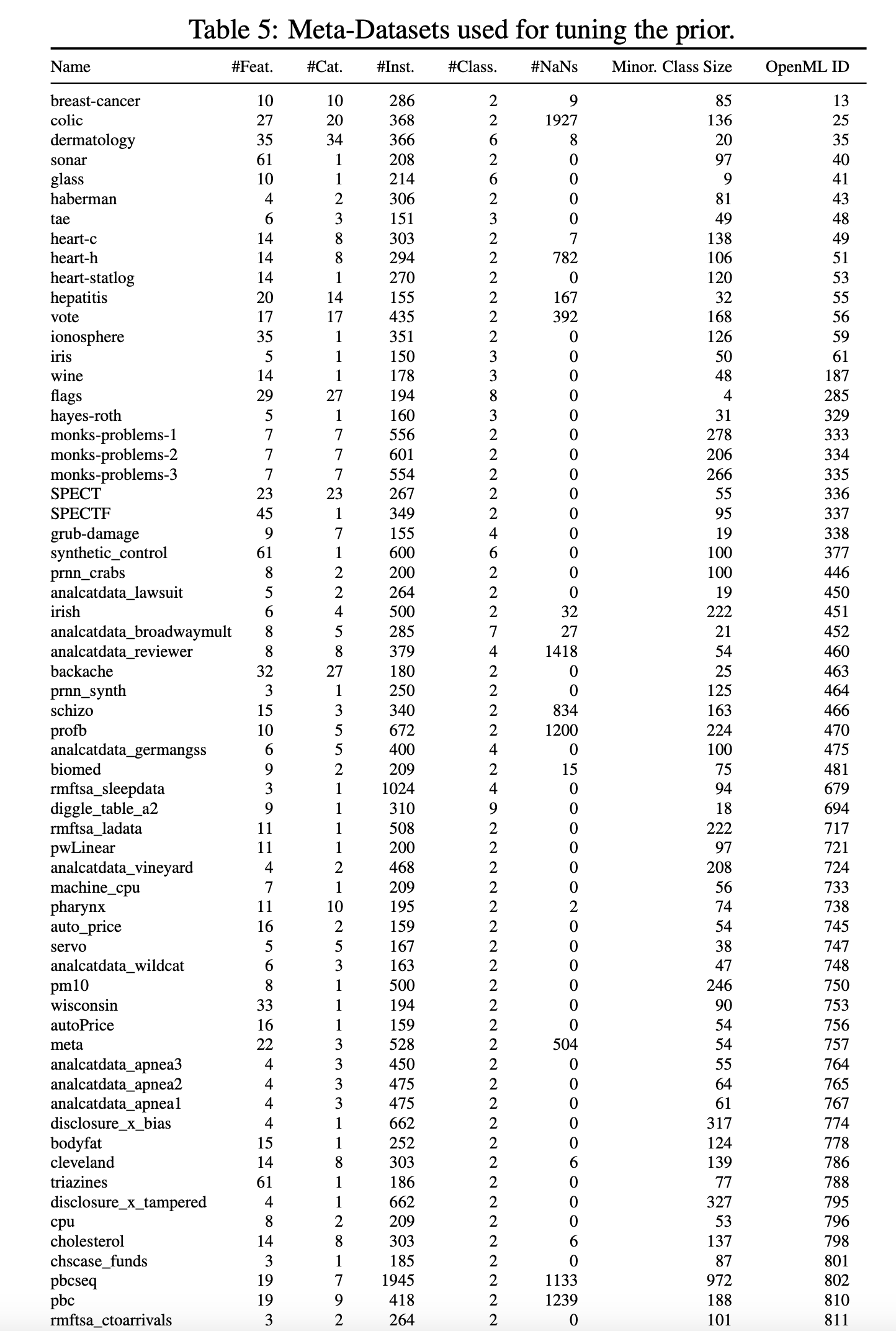
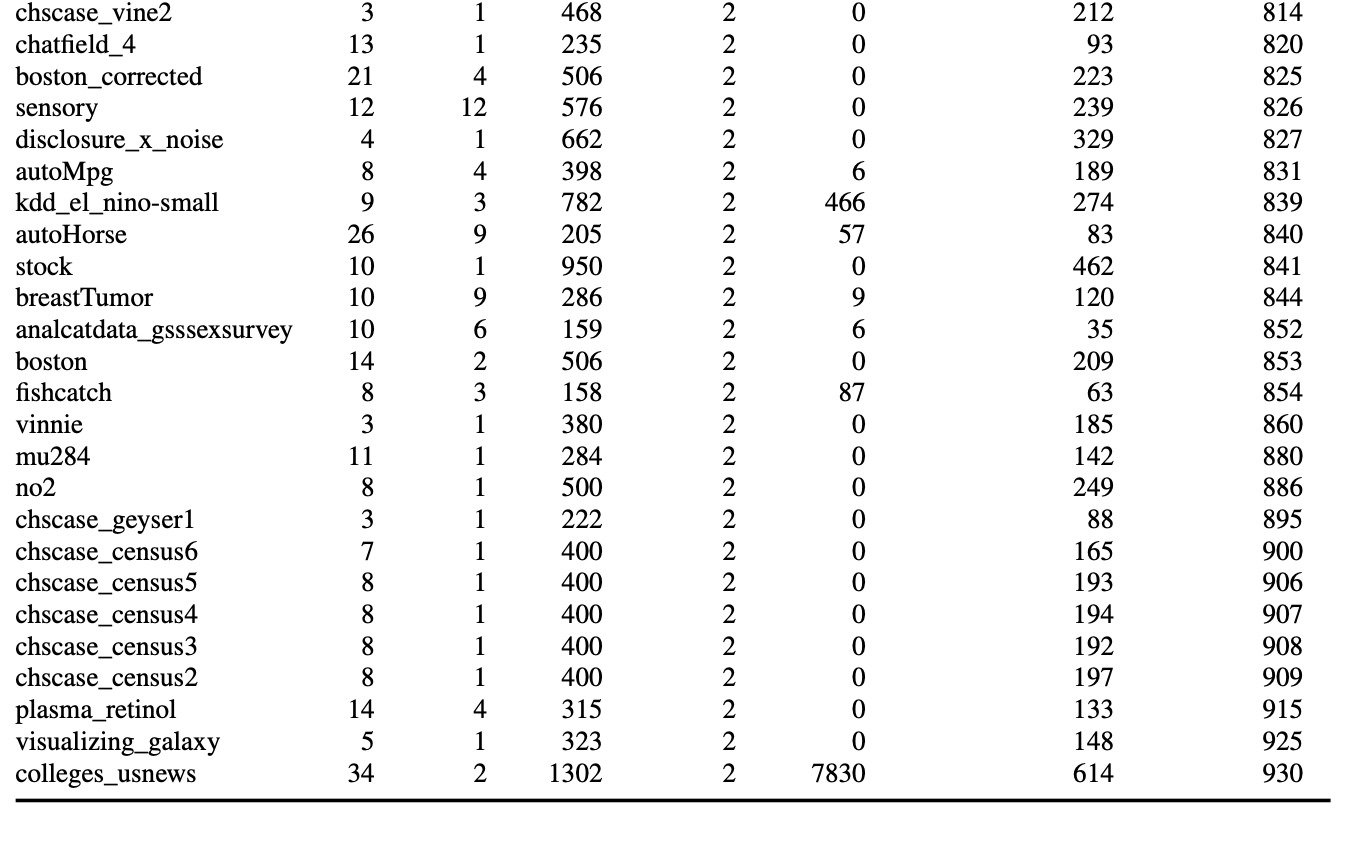
Datasets 테스트 데이터세트로는 2,000개 미만의 샘플, 100개 기능 및 10개 클래스를 포함하는 선별된 오픈 소스 OpenML-CC18 벤치마크 제품군[4]의 모든 데이터세트를 사용했습니다. 결과 세트는 30개의 데이터 세트로 구성되었습니다. 또한 OpenML.org [41, 13]의 150개 검증 데이터 세트의 분리된 세트도 고려했습니다. 이 검증 데이터 세트를 사용하여 방법의 개발과 하이퍼파라미터 분포의 선택을 안내했습니다. 실제 데이터에 앞서 생성된 데이터를 정성적으로 비교하고(그림 3b 참조), 특징 상관관계, 특징 분산, 클래스 분포를 정량적으로 비교하는 방식으로 수행했습니다. 모든 데이터 세트와 수집 방법에 대한 자세한 설명은 부록 G.3에서 확인할 수 있습니다.
Baselines 표 형식 데이터에 대해 5가지 표준 ML 방법과 3가지 최신 AutoML 시스템을 비교했습니다. ML 모델로는 간단하고 빠른 두 가지 기준선인 K-최근이웃(KNN)과 로지스틱 회귀(LogReg)를 고려했습니다. 또한 가우시안 프로세스(GP) [33]와 널리 사용되는 트리 기반 부스팅 방법인 XGBoost [7], LightGBM [? ], CatBoost [32]도 고려했습니다. 각 ML 모델에 대해 5배 교차 검증을 사용하여 주어진 예산이 소진되거나 1,000개의 구성이 평가될 때까지 무작위로 추첨된 구성을 평가했습니다(검색 공간에 대해서는 부록 G.2 참조). 그런 다음 전체 훈련 세트에서 가장 낮은 ROC AUC OVO 오류를 가진 구성을 다시 맞췄습니다. 필요한 경우, 평균, 원핫 인코딩된 범주형 입력 및 정규화된 피처로 결측치를 대입했습니다. 더 복잡하지만 잠재적으로 강력한 기준선으로 세 가지 AutoML 시스템을 선택했습니다: 신경망과 트리 기반 모델을 포함한 ML 모델을 스택 앙상블로 결합하는 AutoGluon [8], 베이지안 최적화를 사용하고 평가된 모델을 가중 앙상블로 결합하는 Auto-sklearn 2.0 [10, 12]. 2 이전 연구에 따르면 DL 기준선은 중소 규모의 표 형식 데이터에 대해 GBDT 또는 AutoML 방법의 성능을 능가하거나 일치하지 않는 것으로 나타났습니다[5, 16, 38]. 또한 TabNet, SAINT, 정규화 칵테일, 비파라미터 변환기[2, 39, 18, 20]와 같은 DL 방법은 훨씬 더 큰 데이터 세트에서 평가되며, 훨씬 더 긴 학습 시간이 필요하고 사용자 지정 파라미터 튜닝 및 전처리를 사용하는 경우가 많습니다. 당사는 여전히 두 가지 대표적인 DL 방법을 평가합니다: 정규화 칵테일과 SAINT [39, 18]입니다.
TabPFN 우리는 특정 주의 마스크가 있고 위치 인코딩이 없는 트랜스포머 인코더[42]를 사용하는 오리지널 PFN 아키텍처[24]를 따릅니다. 이러한 주의 마스크를 약간 수정하여 동일한 성능으로 더 빠르게 추론할 수 있습니다. 또한, 특징을 선형적으로 제로 패딩하고 스케일링하여 특징의 개수가 다른 데이터 세트에서도 모델이 작동할 수 있도록 했습니다. 자세한 내용은 부록 F.2를 참조하세요.
사전 적합 단계에서는 섹션 3에서 설명한 대로 TabPFN을 8개의 GPU에서 20시간 동안 한 번 훈련하여 모든 평가에 사용되는 단일 네트워크를 생성합니다. 이 단계는 비용이 많이 들지만, 알고리즘 개발의 일부로 TabPFN을 위해 오프라인에서 미리 한 번만 수행됩니다. 추론하는 동안 무작위로 회전된 특징 차원과 순열 레이블을 사용하여 z-노멀라이제이션과 앙상블 예측을 적용합니다. 자세한 내용과 사용된 하이퍼파라미터는 부록 F에서 확인할 수 있습니다.
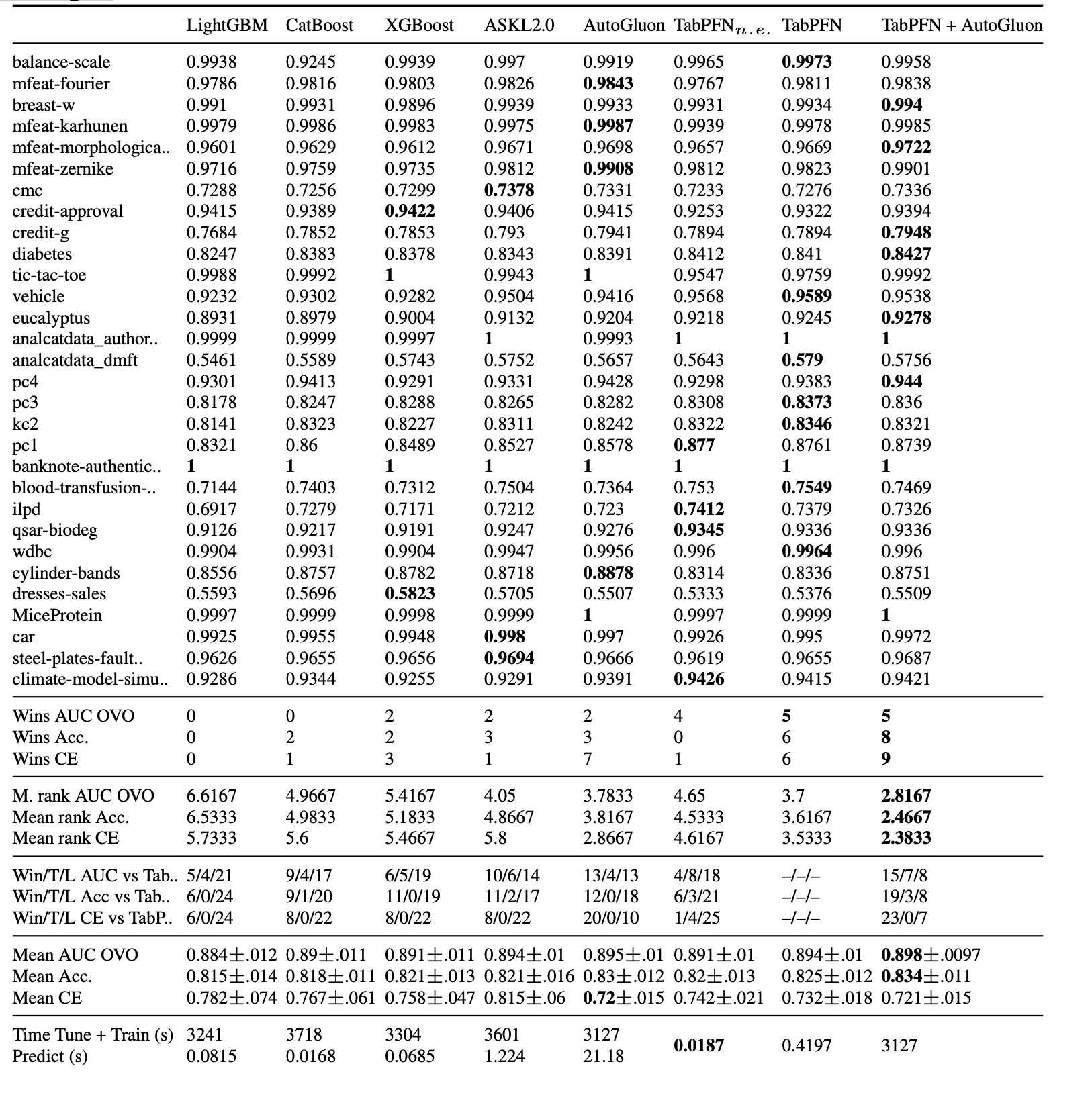
Evaluation Protocol 각 데이터 세트와 방법에 대해 각각 다른 무작위 시드와 다른 훈련 및 테스트 분할을 사용하여 5번의 반복을 평가했습니다(모든 방법은 시드가 주어지면 동일한 분할을 사용했습니다). 데이터 세트 전반의 결과를 집계하기 위해 95% 신뢰 구간을 포함한 ROC AUC(다중 클래스 분류의 경우 일대일(OVO)) 평균, 순위 및 승률을 보고하고 [30, 60, 300, 900, 3600] 초의 예산으로 기준선의 성능과 비교합니다3. 위에서 설명한 대로 앙상블을 위해 32개의 데이터 순열을 사용하여 TabPFN을 실행하고 순열 없이 TabPFN도 평가하며 이를 표 1에서 TabPFN n-e로 레이블을 지정합니다.
Results 그림 5에서 달성한 AUC ROC를 예산의 함수로 표시하여 TabPFN이 다른 모든 방법보다 훨씬 빠르다는 것을 보여줍니다. 하나의 GPU에서 1초 이내에 예측을 수행하여 1시간 학습 후 최고 경쟁사(AutoML 시스템)의 성능과 동등하고 5분 만에 경쟁사의 성능을 압도하는 성능을 달성합니다. 놀랍지 않게도, 단순 기준선(LogReg, KNN)은 적은 예산으로 이미 결과를 얻었지만 예산이 클수록 전반적으로 최악의 성능을 보였습니다. 부스트 트리(XGBoost, CatBoost)는 성능이 더 좋지만, 최첨단 AutoML 시스템인 Auto-sklearn 2.0 및 Autogluon에 비해서는 분명히 성능이 떨어집니다. AutoML 시스템은 더 높은 예산에서 최고의 성능을 발휘하는 기준선입니다.
엔셈블링이 없는 TabPFN은 하나의 데이터 세트를 예측하는 데 GPU에서 0.0187초, CPU에서 0.87초가 소요됩니다. 1분 동안 가장 강력한 기준선과 비슷한 성능을 발휘하며, CPU에서는 70배, GPU에서는 3,200배의 속도 향상을 제공합니다. 더 많은 예산(5분 이상)이 주어지면, 가장 강력한 기준선은 GPU에서 0.42초, CPU에서 16.5초의 시간 예산을 사용하는 기존 TabPFN(앙상블 포함)과 경쟁할 수 있는 성능을 달성합니다. 기준선에 필요한 5분과 TabPFN을 비교하면 CPU에서는 18배, GPU를 사용하면 710배의 속도 향상을 얻을 수 있습니다.
이 시간은 학습된 모델이 이미 메모리에 있고 GPU로 이동했다고 가정한 것으로, 그렇지 않은 경우 0.2초가 소요됩니다. 평균 결과는 표 1에서 확인할 수 있으며, 데이터 세트별 결과를 포함한 자세한 결과는 부록 C.1에서 확인할 수 있습니다.
5 Conclusions & Future Work
표 형식 데이터에 대한 전체 AutoML 프레임워크의 작업을 수행하도록 단일 트랜스포머인 TabPFN을 학습시켜 0.4초 만에 예측을 생성할 수 있으며, 1시간이 지난 후에도 최고 성능의 AutoML 프레임워크가 달성하는 성능과 경쟁할 수 있다는 것을 보여주었습니다. 이 결과는 실시간 예측이 가능하기 때문에 데이터 과학 분야에 지각 변동을 일으킬 수 있습니다. 또한, AutoML의 계산 비용을 절감하여 경제적인 친환경 AutoML을 구현할 수 있습니다.
기본 트랜스포머 아키텍처는 소규모 데이터세트에만 확장할 수 있다는 점, 1000개 미만의 훈련 샘플, 100개의 특징, 10개 클래스로만 구성된 분류 데이터세트에 대한 평가는 부록 A에 자세히 설명되어 있으며, 이는 대규모 데이터세트로 확장하는 작업에 대한 동기를 부여합니다. 또한, 이 작업은 (2) 기존 AutoML 프레임워크에 TabPFN 통합, (3) 시간이 더 주어지면 계속 개선하기 위한 앙상블, (4) 분포 외 견고성 연구, (5) 데이터 세트에 따른 이전 선택, (6) 비표형 데이터로의 일반화 및 (7) 회귀 작업에 관한 여러 가지 흥미로운 후속 연구에 대한 동기를 부여합니다. 거의 즉각적인 최첨단 예측을 제공하는 TabPFN은 (8) 새로운 탐색적 데이터 분석 방법, (9) 새로운 피처 엔지니어링 방법, (10) 새로운 능동 학습 방법도 탄생시킬 수 있을 것입니다. 인과적 추론에 대한 우리의 발전은 (11) SCM의 분포를 고려한 개입 및 반대 사실의 효과 근사치에 대한 후속 연구를 보장합니다.
A Limitations
이 작업에 사용된 트랜스포머 기반 PFN 아키텍처의 런타임과 메모리 사용량은 입력 수, 즉 전달된 훈련 샘플의 수에 따라 4제곱으로 확장됩니다. 따라서 현재 소비자용 GPU에서는 대규모 시퀀스(100,000개 이상)에 대한 추론이 어렵습니다. 이 문제를 해결하고 입력 수에 따라 선형적으로 확장하면서 유사한 성능을 보고하는 방법이 점점 더 많아지고 있습니다[47, 3]. 이러한 방법들은 PFN 아키텍처에 통합될 수 있으며, 따라서 TabPFN에 통합될 수 있습니다. 또한, 실험에서는 섹션 4에서 설명한 대로 특징의 수를 100개로, 클래스의 수를 10개로 제한했습니다. 이 선택은 유연하지만, 우리가 장착한 TabPFN은 이러한 제한을 초과하는 데이터 세트에서는 작동할 수 없습니다.
B Societal Implications
이 연구의 광범위한 사회적 영향 측면에서 볼 때, 예상할 수 있는 매우 부정적인 영향은 보이지 않습니다. 그러나 이 논문은 학습 알고리즘의 탄소 발자국과 접근성에는 긍정적인 영향을 미칠 수 있습니다. 머신러닝 연구에 필요한 계산은 몇 달마다 두 배로 증가하고 있으며, 그 결과 탄소 발자국이 크게 증가하고 있습니다[36]. 또한 계산에 드는 재정적 비용으로 인해 학계, 학생, 연구자들이 이러한 방법을 적용하는 데 어려움을 겪을 수 있습니다. TabPFN이 보여주는 계산 시간 단축은 CO2 배출량과 비용 절감으로 이어지며, 대규모 컴퓨팅에 접근할 수 없는 사용자도 사용할 수 있습니다.
C Additional Results
C.1 Detailed Tabular Results

그림 6에서는 평가되는 데이터 세트의 종류가 기준선과 비교하여 TabPFN의 성능에 어떤 영향을 미치는지 살펴봅니다. 범주형 특징이 없을 때 TabPFN의 성능이 훨씬 더 우수하다는 것을 알 수 있습니다. 이는 범주형 데이터에 더 맞춤화할 수 있도록 이전 작업을 확장해야 한다는 것을 의미합니다. 또한 다중 클래스 설정에서 상대적으로 많은 수의 피처가 제공될 때 TabPFN의 성능이 더 우수하다는 것을 알 수 있었습니다.
4.2절의 본문의 결과 외에도 표 1에서 다양한 성능 값과 데이터 세트별 결과를 보고합니다.
표 1: 표 1: 데이터 세트당 및 분할당 요청된 시간 60분 동안의 소규모 OpenML-CC18에 대한 ROC AUC OVO 결과. 가능한 경우, 모든 기준선은 ROC AUC 최적화를 목표로 삼고 다른 기준선은 CE 최적화를 목표로 삼았습니다. 전체적으로 각 방법에는 150시간의 시간 예산이 주어졌지만 모든 방법이 전체 예산을 사용한 것은 아닙니다.
D. Details of the TabPFN Prior
D.1SCM Prior
The Sampling Algorithm MLP 아키텍처로 시작하여 가중치를 떨어뜨려 효율적으로 샘플링할 수 있는 DAG의 하위 패밀리를 인스턴스화합니다. 즉, k개의 특징과 n개의 샘플이 있는 데이터셋을 샘플링하려면 각 데이터셋에 대해 다음 단계를 수행합니다:
(1) MLP 레이어 수 l ∼ p(l) 및 노드 수 h ∼ p(h)를 샘플링하고 숨겨진 크기 h를 가진 l 계층 MLP처럼 구조화된 그래프 G(Z, E)를 샘플링합니다.
(2) 각 에지마다 가중치를 샘플로 추출합니다.
(3) 임의의 에지 집합 e ∈ E를 드롭하여 임의의 DAG를 생성합니다.
(4) 노드 Z에서 특징 노드 Nx와 라벨 노드 Ny의 집합을 샘플링합니다.
(5) 메타 분포에서 잡음 분포 p(ε) ∼ p(p(ε))를 샘플링하여 SCM을 생성합니다,
모든 fi가 무작위 아핀 매핑으로 인스턴스화되고 활성화됩니다. 각 zi는 MLP에서 희소하게 연결된 뉴런에 해당합니다.
위의 매개변수가 고정된 상태에서 데이터 세트의 각 구성원에 대해 다음 단계를 수행합니다. (1) 특정 분포에서 노이즈 변수 εi를 샘플링합니다.
(2) zi = a((Pj∈PAG(i) Eijzj) + εi)를 사용하여 모든 z ∈ Z의 값을 계산합니다.
(3) 특징 노드 Nx와 출력 노드 Ny에서 값을 검색하여 반환합니다.
데이터 세트당 하나의 활성화 함수를 {ReLU,Tanh,Identity}에서 샘플링합니다[25]. 레이어 수 p(l) 및 노드 수 p(h)에 대한 샘플링 방식은 로그 정규 분포를 따르고, 탈락률은 베타 분포를 따르며, p(p(ε))는 정규 분포의 평균과 표준 편차를 갖는 정규 분포를 샘플링하도록 설계되었습니다.
D.2 Tabular Data Refinements
Tabular 데이터 세트는 특징 유형이 숫자, 서수 또는 범주형일 수 있고 특징 값이 누락되어 특징이 희박해질 수 있는 등 다양한 특성으로 구성됩니다. 다음 섹션에서 설명하는 대로 이러한 특성을 이전 설계에 반영하려고 합니다.
D.2.1 Preprocessing
메타 훈련 중에 입력 데이터는 평균과 분산이 0이 되도록 정규화되며, 실제 데이터로 평가할 때도 동일한 단계를 적용합니다. 표 형식 데이터에는 메타 학습 중에는 존재하지 않을 수 있는 기하급수적으로 스케일링된 데이터가 포함되는 경우가 많으므로 추론 중에 파워 스케일링을 적용합니다[46]. 따라서 실제 표 형식 데이터 세트에서 추론하는 동안 기능은 메타 학습 중에 보이는 것과 더 가깝게 일치합니다. z-통계, 파워 변환 및 기타 모든 전처리를 계산할 때는 훈련 샘플만 사용합니다. 이 전처리 시간은 우리 방법의 추론 시간을 보고할 때 고려됩니다.
D.2.2 Correlated Features
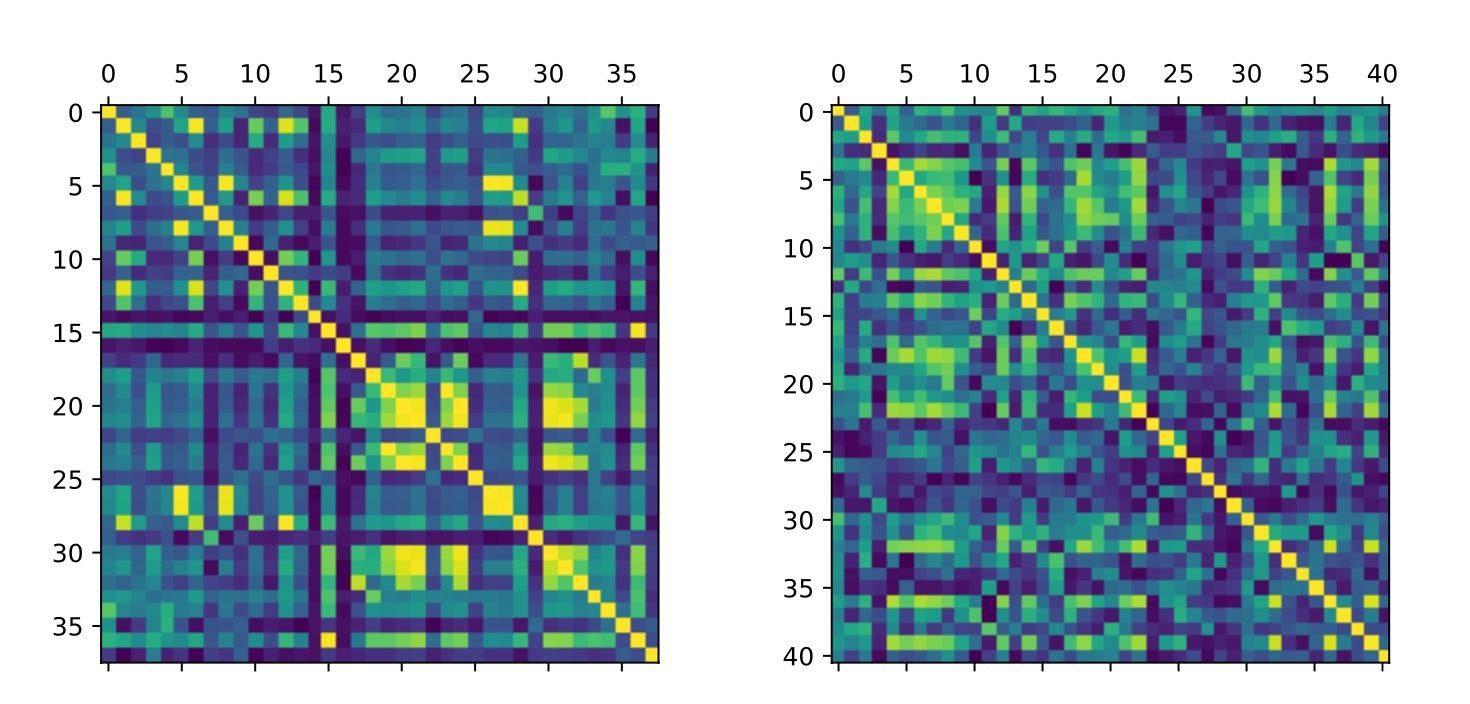
표 형식 데이터의 특징 상관관계는 데이터 세트마다 다르며 독립적인 것부터 높은 상관관계까지 다양합니다. 이는 기존의 딥러닝 방법에 문제를 야기합니다[5]. 대규모 SCM 공간을 고려할 때 다양한 정도의 상관관계가 있는 특징이 자연스럽게 선행에 발생합니다. 또한, 실제 표 형식의 데이터에서는 특징의 순서가 비정형적인 경우가 많지만 인접한 특징이 다른 특징보다 더 높은 상관관계를 갖는 경우가 많습니다. 따라서 "블록 단위 피처 샘플링"을 사용하여 정렬된 피처 간의 상관관계 구조를 반영합니다. 우리의 SCM 생성 방법은 이를 위한 방법을 자연스럽게 제공합니다. SCM 생성의 첫 번째 단계는 한 계층의 노드가 이전 계층으로부터만 입력을 받을 수 있는 단방향 계층 네트워크 구조를 생성하는 것입니다. 따라서 한 계층의 특징들은 상관관계가 높은 경향이 있습니다. 우리는 계층화된 네트워크 구조에서 인접한 노드를 블록 단위로 샘플링하고 이렇게 정렬된 블록을 특징 집합에 사용하는 방식으로 이를 활용합니다. 그림 7에서는 이렇게 생성된 데이터 세트(오른쪽)의 상관관계를 시각화하고 실제 데이터 세트(왼쪽)와 비교하여, 우리의 사전 작업이 실제 데이터 세트와 유사한 상관관계 구조를 산출한다는 것을 보여줍니다.
D.2.3 Generating irregular functions
실제 데이터에서는 일부 특징이 다른 특징보다 일관되게 더 중요합니다. 무작위로 네트워크 가중치를 초기화하면 특징의 중요도가 조금씩 달라지지만, 숨겨진 차원이 증가하면 입력 특징의 평균 효과는 평균으로 회귀합니다. 각 입력 피처에 대한 가중치 매개변수를 샘플링하고 모든 출력 가중치에 이 계수를 곱하여 차이를 증폭합니다. 앞에서는 그래프의 연결을 무작위로 스파스화했습니다. 따라서 숨겨진 변수와 출력 노드는 단계당 더 적은 수의 매개변수의 영향을 받아 더 많은 수의 매개변수가 다시 평균으로 회귀하기 때문에 더 불규칙한 패턴을 생성합니다. 여기서는 스파스화를 변수 블록으로 확장하여 일부 변수 그룹이 더 강력하게 상호 작용하도록 유도합니다. 또한 노이즈 변수를 샘플링하는 방식도 확장합니다. 각 노드의 가우스 노이즈를 동일한 분포에서 샘플링하는 대신, 먼저 각 노드의 노이즈 평균과 표준 편차를 샘플링한 다음 이 분포에서 샘플링합니다. 또한 실제 데이터에서 관찰되는 것처럼 불균일하게 분포된 입력 데이터 x를 생성합니다. 네트워크를 통해 전파되는 입력 변수 x는 가우스 분포, 집피안 분포, 다변량 분포와 같은 다양한 분포에서 샘플링합니다.
D.2.4 Nan Handling
이전 모델에서 결측값을 모델링하기 위해, 사전 훈련 중에 확률적으로 결측값을 도입합니다. 각 데이터 세트에 대해 누락된 특징이 포함될지 여부를 나타내는 이진 의사 결정 변수 M을 샘플링한 다음, 누락된 값의 분수 fm을 샘플링합니다. M이 양수이면 특징값의 일부분 fm을 무작위로 균일하게 삭제합니다. 누락된 값의 위치를 나타내는 이진 누락 값 마스크를 도입하여 특징 임베딩과 함께 모델에 전달합니다. 합성 데이터에 대한 메타트레이닝과 실제 데이터 세트에 대한 추론 과정에서 이 마스크를 추가합니다.
D.2.5 Categorical Features
Tabular데이터에는 숫자 특징뿐만 아니라 불연속적인 범주형 특징도 포함되는 경우가 많습니다. 범주형 특징은 순서를 정할 수 있습니다. 즉, 범주는 일부 기본 변수의 구간차원을 나타내거나 섞여 있을 수 있습니다. 데이터 세트당 범주형 특징의 무작위 분수 pcat(하이퍼파라미터)를 선택해 범주형 특징을 도입합니다. 숫자 클래스 레이블을 불연속형 다중 클래스 레이블로 변환하는 것과 유사하게, 밀집형 특징을 불연속형 특징으로 변환합니다. 또한 다중 클래스 레이블과 유사하게, 범주형 특징의 셔플 프랙션 pscat을 선택해 카테고리를 재구성합니다. 자세한 내용은 3.5를 참조하세요. 그러나 범주형 특징에 관한 실험에서는 큰 개선이 나타나지 않았습니다. 범주형 특징을 처리하는 더 적절한 방법을 찾는 것이 앞으로의 연구 과제가 될 수 있습니다.
E Details of Prior-Data Fitted Network Algorithm

F Setup of our method
F.1 Transformer Hyperparameters
12개의 레이어, 임베딩 크기 512, 피드포워드 레이어에 숨겨진 크기 1024, 4헤드 주의가 있는 PFN 트랜스포머만 고려했습니다. 각 훈련에 대해 {.001, .0003, .0001}의 3가지 학습률 세트를 테스트하고 최종 훈련 손실이 가장 낮은 것을 사용했습니다. 결과 모델에는 25.82M개의 파라미터가 포함되어 있습니다.
F.2 PFN Architecture Adaptations
Attention Adaption 기존 PFN 아키텍처[24]는 단일 멀티헤드 자기 주의 모듈[42]을 사용하여 모든 훈련 예제 간의 주의와 검증 예제에서 훈련 예제로의 주의까지 계산합니다. 이를 가중치를 공유하는 두 개의 모듈로 대체했는데, 하나는 훈련 예제 간의 자체 주의도를 계산하고 다른 하나는 검증 예제에서 훈련 예제로의 교차 주의도만 계산합니다. 개념적으로 이는 다음 예제에서처럼 모든 것이 스스로 주의하도록 허용하는(대각선은 1) 원래 아키텍처와는 약간 다른 자기 주의 마스크를 사용하는 것과 같습니다.
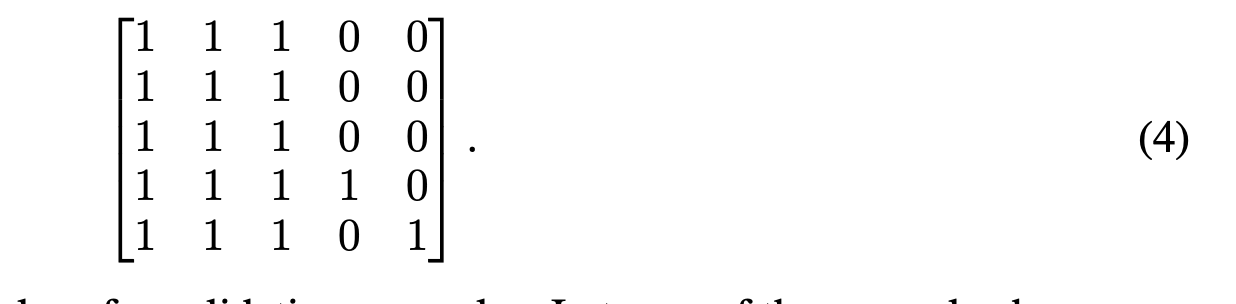
유효성 검사 예제에서는 자체에 대한 주의를 제거합니다. 위의 예제에서는

하지만 현재 위치의 상태에 대한 정보는 여전히 잔여 지점을 통해 흐릅니다.
Flexible Encoder 데이터 세트는 입력 차원(특징)의 수가 같지 않은 반면, PFN은 고정 차원 입력을 허용하는 인코더 레이어를 사용합니다. 여기서는 차원 수가 서로 다른 데이터셋을 단일 PFN으로 모델링하는 방법을 설명합니다. 훈련 중에 데이터셋의 차원 수를 최대 100까지 무작위로 균일하게 뽑습니다. 데이터 세트의 특징 수 k가 최대 특징 수 K보다 작은 경우 데이터 세트를 제로 패딩하고 이러한 특징의 크기를 Kk만큼 스케일링함으로써 다양한 특징 수로 훈련 및 추론할 수 있도록 인코더가 변경됩니다(단, 크기는 동일하게 유지됨).
F.3 TabPFN Training
512개의 데이터 세트로 18,000개의 단계로 최종 모델을 훈련했습니다. 즉, 합성으로 생성된 9216,000개의 데이터세트로 TabPFN을 훈련한 것입니다. 이 훈련은 8개의 GPU(Nvidia RTX 2080 Ti)에서 20시간이 걸렸습니다. 각 데이터 세트의 크기는 1024로 고정되어 있으며, 무작위로 균일하게 훈련과 검증으로 나눴습니다. 일반적으로 약 1,000만 개의 데이터 세트 이후에는 학습 곡선이 평평해지는 경향을 보였으며 일반적으로 노이즈가 매우 심했습니다. 이는 아마도 이전에 다양한 데이터 세트를 생성했기 때문일 것입니다.
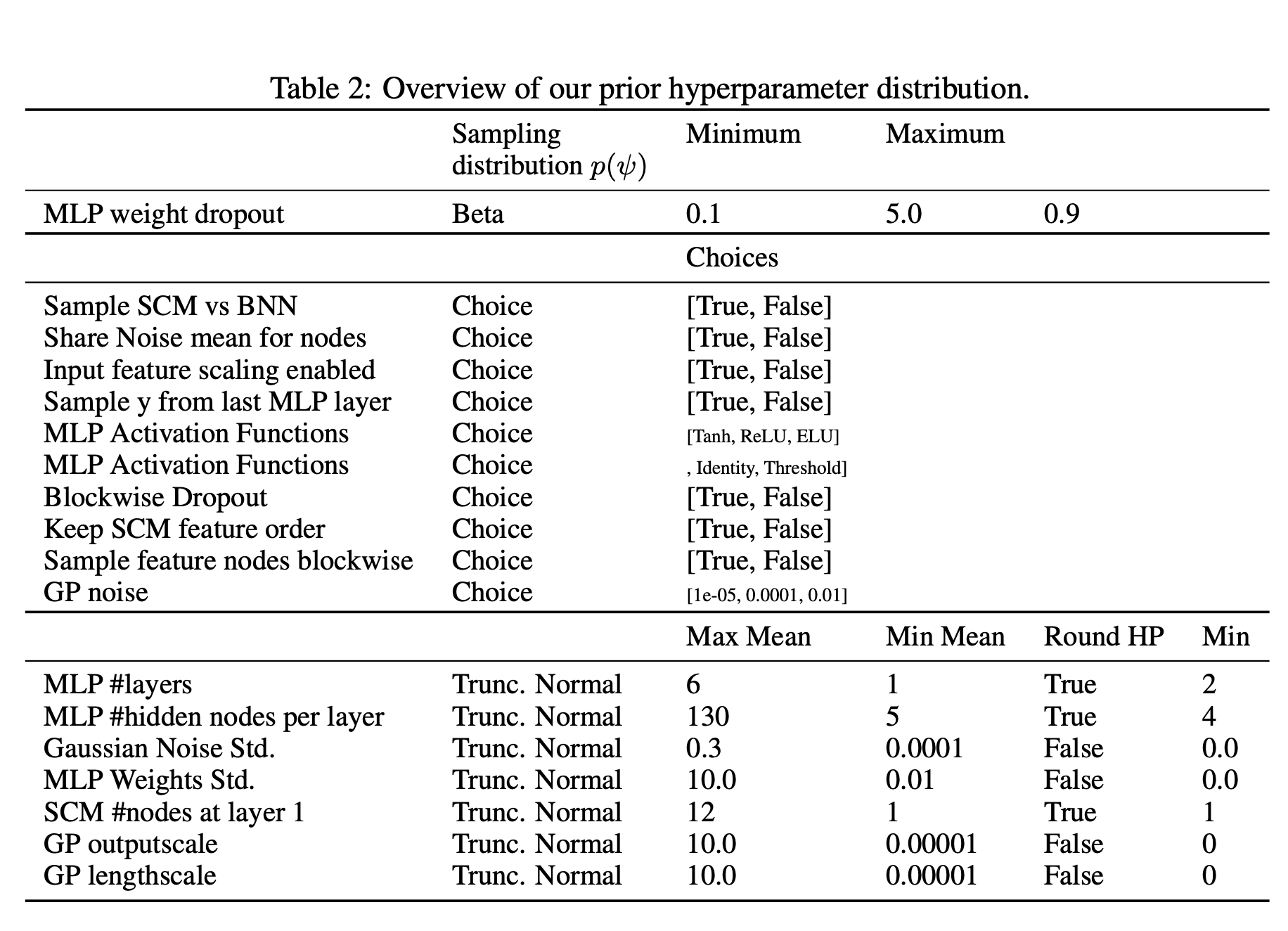
F.4 Prior Hyperparameters
G Details for Tabular Experiments
여기에서는 본문의 섹션 4에서 수행한 실험에 대한 추가 세부 정보를 제공합니다.
G.1 Hardware Setup
기준선을 포함한 모든 평가는 인텔(R) 제온(R) 골드 6242 CPU(2.80GHz)가 장착된 컴퓨팅 클러스터에서 CPU 1개와 최대 6GB RAM을 사용하여 실행되었습니다. TabPFN을 사용한 평가에는 RTX 2080 Ti를 추가로 사용했습니다.
G.2 Baselines
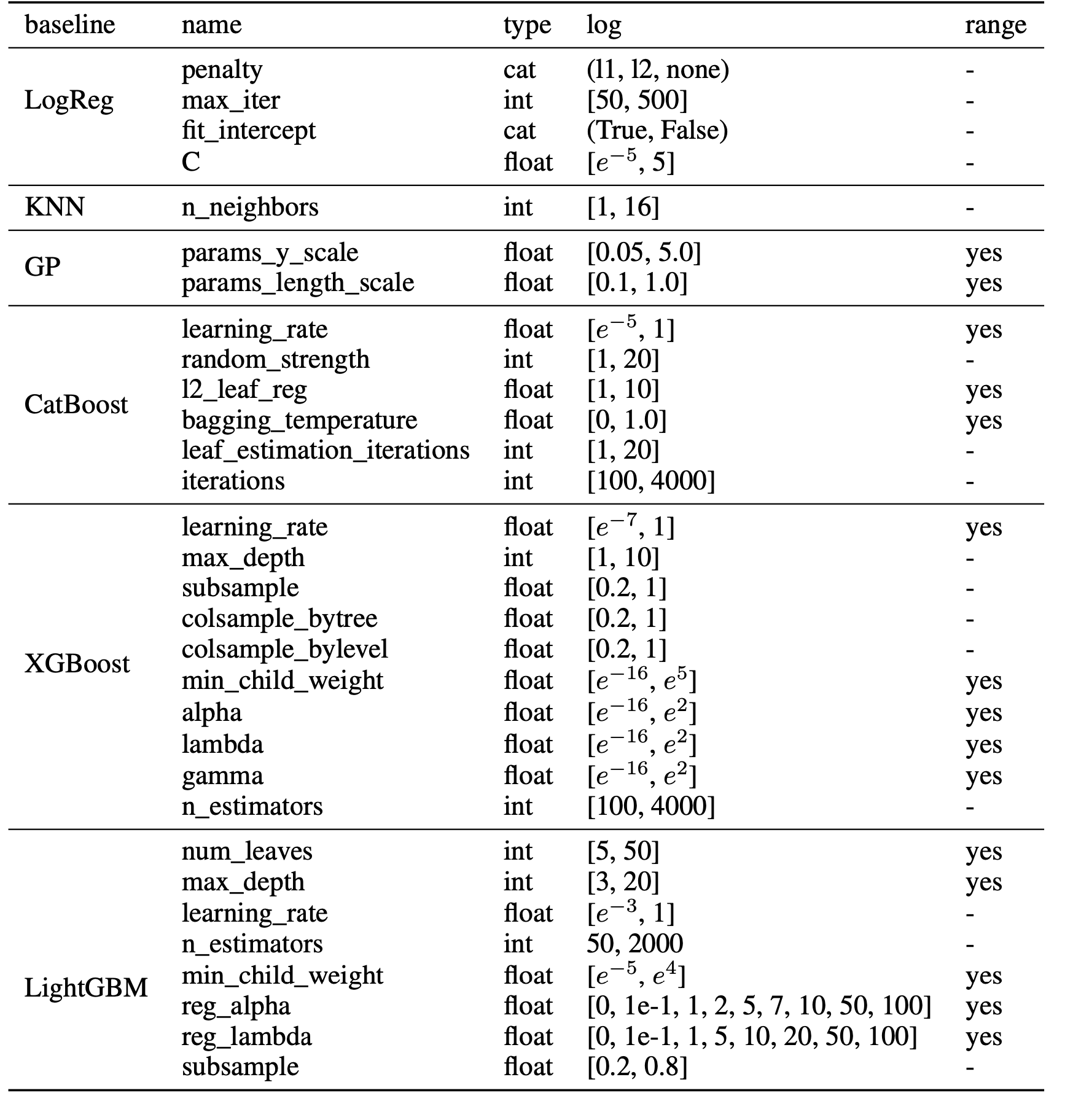
기준선을 조정하는 데 사용된 검색 공간은 표 3에 나와 있습니다. CatBoost와 XGBBoost의 경우, 다음과 같은 예외를 제외하고 Shwartz-Ziv 및 Armon [38]과 동일한 범위를 사용했습니다: CatBoost의 경우 문서에 없기 때문에 최대 깊이 하이퍼파라미터를 제거했고, CatBoost와 XGBBoost의 경우 n_estimators의 범위를 [100, 4000] 범위로 설정했습니다. KNN, GP 및 로지스틱 회귀 기준선을 위한 검색 공간은 처음부터 설계되었으며, scikit-learn [30]의 각 구현을 사용했습니다. CatBoost와 AutoSklearn의 경우 범주형 특징의 위치를 분류기에 전달합니다(AutoGluon은 범주형 특징 열을 자동으로 감지합니다). 로지스틱 회귀, GP 및 KNN에 대한 입력은 최소 최대 스케일링을 사용하여 [0, 1] 범위로 정규화합니다.
G.3 Used Datasets
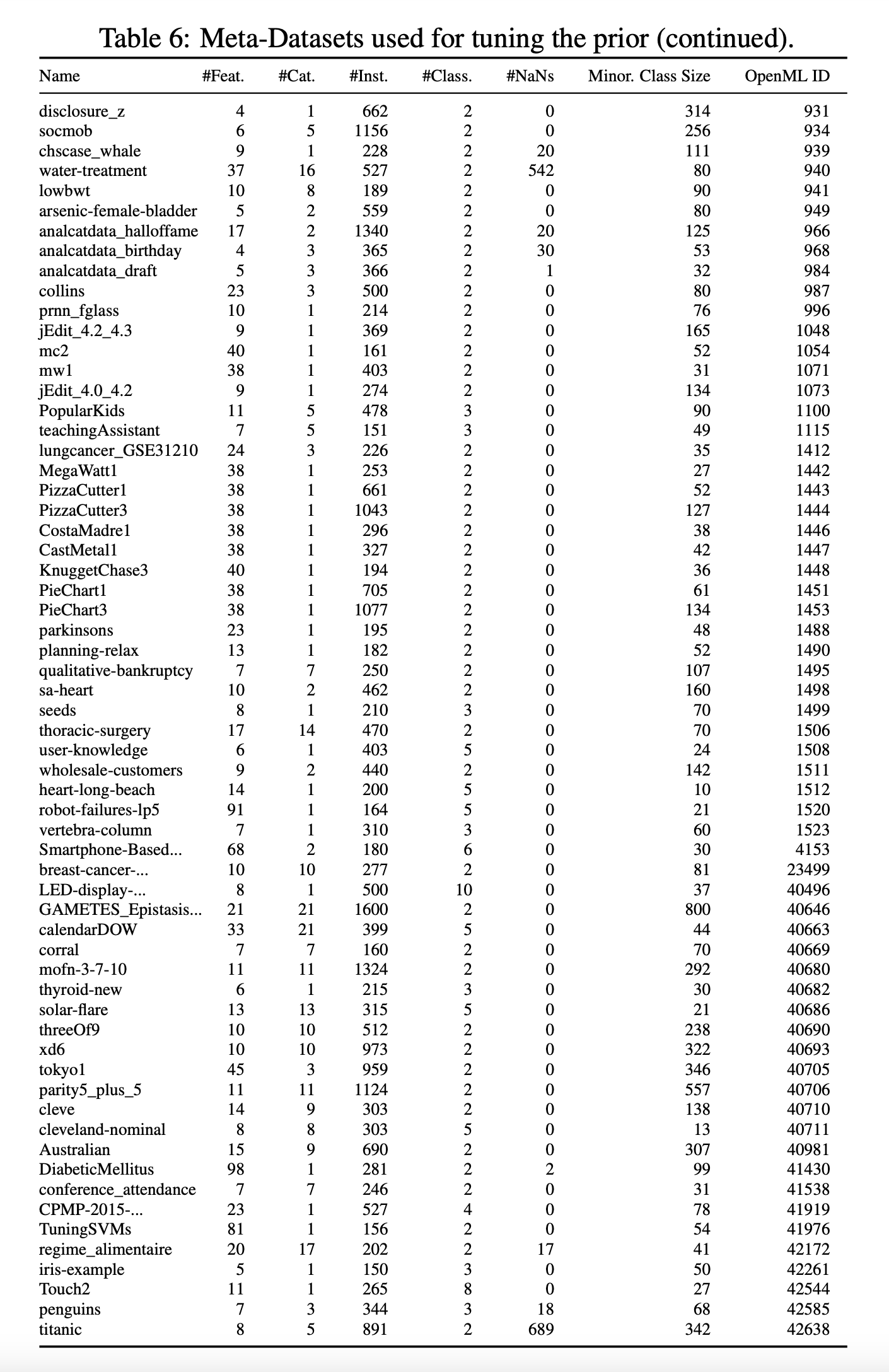
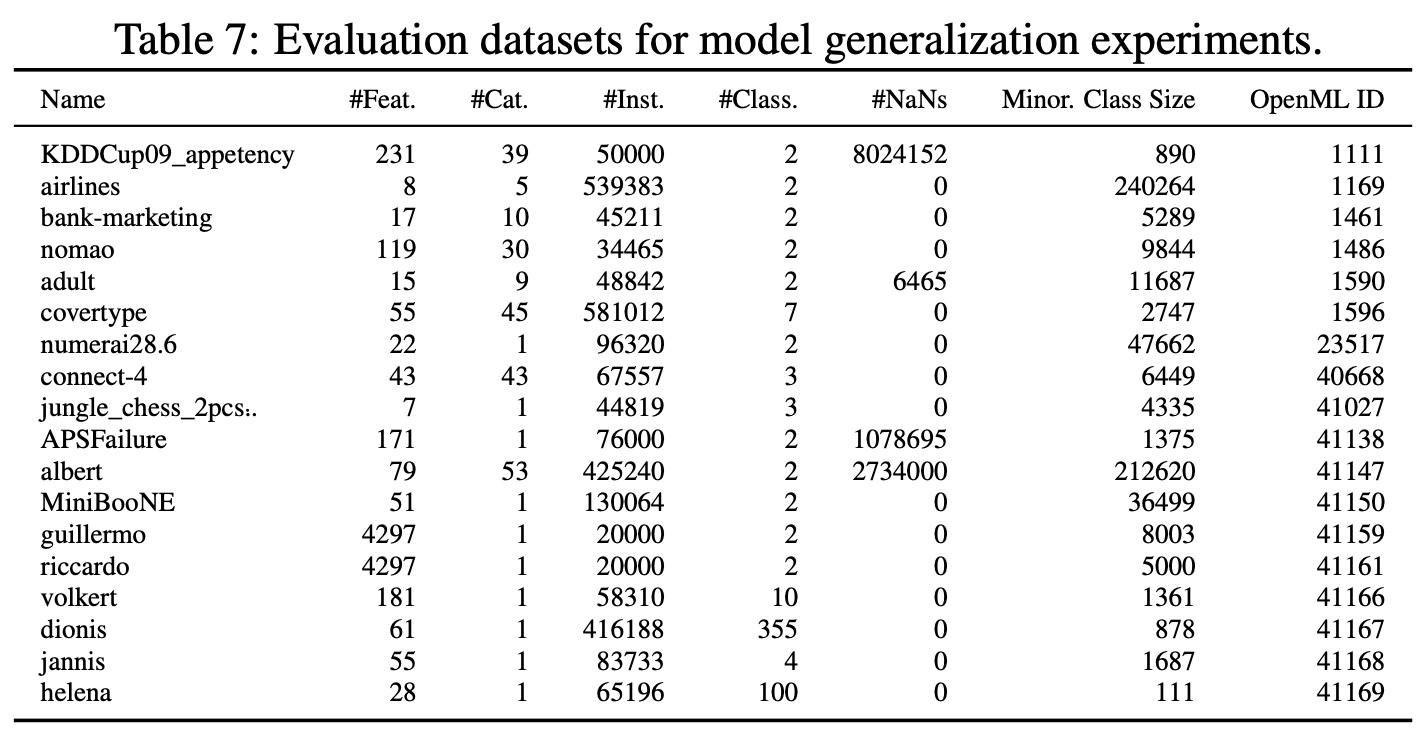
저희는 방법을 구성하고 평가하기 위해 세 개의 서로 다른 데이터 세트 세트를 사용합니다. 테스트 세트(표 4 참조), OpenML-CC18 벤치마크 제품군[4]의 하위 세트, OpenML.org[41]에서 수집한 메타 세트(표 5 및 6 참조)가 그것입니다. 이들은 BSD 3 조항 라이선스에 따라 라이선스가 부여됩니다.
테스트 세트의 경우, 샘플 수가 2,000개, 기능 수가 100개 또는 클래스 수가 10개 미만인 OpenML-CC18 벤치마크 제품군의 모든 데이터 세트를 고려했으며, 그 결과 작은 표 형식의 데이터 세트를 나타내는 30개의 데이터 세트가 남게 되었습니다. 메타 세트의 경우, OpenML.org의 모든 데이터 세트를 고려하고 다음과 같은 필터링 절차를 적용했습니다: 테스트 세트에 포함된 모든 데이터 세트와 샘플이 1,000개, 기능이 100개 또는 클래스가 10개 이상인 모든 데이터 세트를 삭제했습니다. 또한 중복 여부를 수동으로 확인하고 피처, 클래스 및 샘플 수가 테스트 세트의 데이터 세트와 동일한 데이터 세트를 제거했습니다. 또한 시계열 데이터 세트인 FOREX와 인위적으로 생성한 데이터 세트(예: Univ 및 Friedman 데이터 세트)도 수동으로 삭제했습니다. 나머지 메타 세트는 150개의 데이터 세트로 구성됩니다.
H Code
실험 및 사전 학습된 모델을 재현하기 위한 노트북과 함께 코드는 https://anonymous.4open.science/r/TabPFN-2AEE 에서 확인할 수 있습니다.또한 두 개의 데모도 만들었습니다. 하나는 TabPFN 예측을 실험하는 데모(https:// huggingface.co/spaces/TabPFN/TabPFNPrediction)이고 다른 하나는 새로운 데이터 세트에 대한 교차 검증 ROC AUC 점수를 확인하는 데모(https://huggingface.co/spaces/TabPFN/TabPFNEvaluation)로, 모두 저사양 CPU에서 실행되므로 약간의 시간이 소요될 수 있습니다. 두 데모는 모두 scikit-learn 인터페이스를 기반으로 하며, 이를 통해 사용자는 scikit-learn SVM처럼 쉽게 TabPFN을 사용할 수 있습니다.
Table 3: Hyperparameter spaces for baselines. All, except LightGBM, adapted from Shwartz-Ziv and Armon [38].